أنواع الزوايا وقياسها
أنواع الزوايا وقياسها إن للزوايا أهمية كبيرة في مادة الرياضيات، فهناك العديد من المفاهيم الخاصة بالمادة والتي يكون من ضمنها هذا المفهوم، لذلك سنعرض ما يخص أنواع الزوايا وقياسها.
وكيفية التعبير عنها، لكي نتمكن من قياس أي زاوية مهما كانت، لهذا لابد من متابعة هذا المقال أنواع الزوايا وقياسها.
ما هو تعريف الزاوية؟
- إن الزاوية هي مسافة محصورة ومتواجدة عبر التلاقي الحادث بين مستقيمين، ونجد أن المستقيمان هما الضلعين المكونان للزاوية، فهما شعاعان تشكلان من أجل الزاوية، وتسمى عن طريق ثلاثة حروف.
ما هي أنواع الزوايا بالتفصيل؟
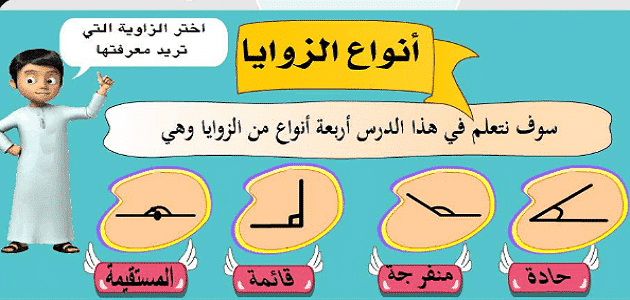
أنواع الزوايا وقياسها نجد أن الزوايا تعرف وتصنف من خلال درجاتها، وسنجد أن من هذه الزوايا هي:
زاوية قائمة
- نجد أن قياس هذه الزاوية هو ٩٠ درجة، وهذا يمكن اكتشافه بكل سهولة من خلال مثلث ويكون قائم، بحيث إن تم وضعه على هذه الزاوية ووجدنا أن هناك تطابق بينهم فإن هذه الزاوية تكون قائمة أي قياسها ٩٠ درجة.
شاهد أيضًا : كيفية تنظيم الوقت للمذاكرة الناجحة للحفظ والفهم
زاوية حادة
- نجد أن هذه الزاوية تتراوح من بين الصفر إلى ما هو أصغر من ٩٠، فلابد أن تكون صغيرة عن القائمة لكي تكون زاوية حادة، وعند وضع نفس المثلث القائم نرى هذا الصغر واضح من خلال المثلث، إذًا تكون هذه الزاوية حادة.
زاوية منفرجة
- نجد هنا في هذه الزاوية أنه عند قياس الزاوية، نجدها كبيرة عن الزوايا السابقة، فهي تكون أكبر من ٩٠ درجة، ولكنها أصغر من ١٨٠ درجة، إذًا نجد أن قياسها سيكون كبير عن المثلث القائم المستخدم للقياس.
زاوية مستقيمة
- نرى هنا في هذه الزاوية أنها أصبحت أكبر من الزوايا السابقة، فهي تكون درجتها ١٨٠ درجة، وهي بالفعل مستقيمة.
زاوية منعكسة
- تكبر هذه الزاوية عن ١٨٠ درجة، ولكنها تكون صغيرة عن ٣٦٠ درجة، فهي هنا تكون محصورة بين الزاوية المستقيمة والزاوية الكاملة.
زاوية كاملة
- نجد هنا في هذه الزاوية أن قياسها قد اكتمل ب٣٦٠ درجة، فهي تكون لها دورة بشكل كامل لذلك تسمى بالكاملة، فعندما تبدأ من نقطة تعود إليها من جديد.
أمثلة على بعض أنواع الزوايا وطريقة حلها
مثلًا عند وجود زاوية معينة ونريد أن نعرف ما هي نوع الزاوية فيكون ذلك من خلال عدة ملاحظات سوف نعرف هنا:
- زاوية قياسها ٢٠ درجة: هنا نجد أنها تكبر عن الصفر، ولكنها تصغر عن ٩٠ درجة فهي إذن تصنف مع الزاوية الحادة.
- وزاوية قياسها ٩٥: هي زاوية تكبر عن ٩٠ درجة ولكنها تصغر عن ١٨٠ درجة، فهي إذن تسمى بزاوية منفرجة.
- زاوية قياسها ٣٦٠: نجد أنها كاملة فهي تكبر عن جميع قياسات الزوايا، إذن تسمى بزاوية كاملة.
- زاوية قياسها ١٨٣: نرى أنها تكبر عن ١٨٠، ولكنها تصغر عن ٣٦٠ إذن هذه الزاوية هي منعكسة.
- وزاوية قياسها ١٠: هذه الزاوية تكون كبيرة عن الصفر، ولكنها تصغر عن ٩٠ إذن تسمى بهذا القياس زاوية حادة.
- زاوية قياسها ٢٣٠: تكبر هذه الزاوية عن ١٨٠، ولكنها تصغر عن ٣٦٠، إذن هي زاوية منعكسة.
- زاوية قياسها ١٠١: نجد أنها تكبر عن ٩٠ درجة، ولكنها تصغر عن ١٨٠ درجة ونجد أن بذلك تصبح معروفة باسم زاوية منفرجة.
- ونستمر في رؤية قياسات الزوايا كما في الأمثلة، ونحدد الزاوية هل هي كبيرة من ماذا وصغيرة من ماذا، وعند معرفة هذه القاعدة سنتمكن من معرفة نوع الزاوية بكل سهولة، ولكن إن وجدت زاوية أكبر من ٣٦٠ وليكن ٣٧٠ فنجد أنها لا تكون تابعة لقياس ما بين الصفر و٣٦٠ درجة.
كيف نتمكن من رسم الزاوية؟
إن كان لدينا قياس معروف لزاوية، أيضًا ولدينا مسطرة ومنقلة، فهكذا يصبح الأمر أبسط، ويجعلنا نتمكن من رسم أي زاوية فقط نمشي مع الخطوات لكي تكون النتيجة صحيحة.
وبدون أي خطأ، فإن كان هناك زاوية قياسها ٥٥ درجة وأردنا قياسها.
فما علينا إلا إتباع الاتي وسوف نكون على علم برسم أي زاوية مهما كان قياسها:
- لابد من وجود المنقلة والمسطرة فلا يمكن البدء من دونهم، أو القياس بدونهم، واستخدامهم يكون بكل دقة لكي يكون الناتج صحيح.
- نبدأ عبر استخدام المسطرة والقلم الرصاص برسم قطعة تكون مستقيمة على الورق.
- ونسميها بالقطعة أ س ونحدد أ في بداية القطعة و س في نهاية القطعة.
- نضع بعد ذلك المنقلة على هذه القطعة المسماة أ س، بحيث يكون المركز على النقطة س.
- بعد وضع المنقلة التي تكون على القطعة تمامًا.
- نقوم بمعرفة رقم ٥٥ المتواجد عليها ونحددها بكل دقة.
- نقوم بوضع نقطة على الورقة بحيث تكون أمام رقم الزاوية ونقوم بتسمية هذه النقطة وليكن د.
- ونقوم بعد ذلك باستخدام المسطرة بتوصيل النقطة د بالنقطة س.
- ثم نجد أننا كونا زاوية أ س د، قياسها ٥٥ درجة، باستخدام المنقلة وبدون أي أخطاء.
شاهد أيضًا : كيفية عمل جدول للمذاكرة اليومية لكل المراحل
المنقلة واستخدامها
إن المنقلة أداة مرقمة بأرقام تسهل قراءتها بكل سهولة، بحيث نجد أن المنقلة هامة في قياس الزوايا.
فهي مرقمة بكل الأرقام من بداية الصفر إلى ٣٦٠ درجة، بذلك يمكن قراءة كل الزوايا.
وعندما نضعها بطريقة صحيحة سنجد أننا قد توصلنا إلى قياس دقيق، وتكون الطريقة الصحيحة كالأتي:
- عندما نجد أ ج د ونريد أن نستعمل المنقلة في قياس الزاوية.
- فكل ما علينا فعله هو وضع المنقلة على الزاوية ج ثم نقوم بالقراءة.
- ويكون الرقم الموجود أمام الضلع هو قياس الزاوية، لذلك نجد أن للمنقلة أهمية كبيرة في قياس الزوايا وليس للرسم فقط.
هل هناك مسميات أخرى للزوايا لا نعرفها؟
نعم يوجد مسميات منها:
زاويتان متجاورتان
- يكون هذا الاسم خاص بكل زاويتين يكون لها نفس الرأس.
- وأيضًا أحد الأضلاع، ولكن الضلعان الآخران يكونان في جانب مختلف.
زاويتان متتامتان
- نجد أن هذا الاسم ينطبق على كل زاويتين يكون مجموعهم زاوية قائمة أي يكون المجموع هو ٩٠ درجة.
زاويتان متكاملتان
- نجد أنهم زاويتان عند جمعهم نجدهم ١٨٠، فهما هنا يشكلان مجموع الزاوية المستقيمة.
زاوية منعدمة
- نجد أن هذا الاسم ينطبق على الزاوية التي تكون صفر، لذلك تسمى منعدمة أي بدون قياس.
زاويتان مشتركان في الرأس
- نجد أن هذا يكون من خلال اشتراكهم في الأضلاع والرأس.
زوايا متبادلة بالرأس
- فنرى أن ما يكون داخليًا يسمى بالزوايا الداخلية، وعند تواجدهم في حالة تقابل يسميان متبادلتان.ز
- وهناك زوايا متناظرة أيضًا يكونان، بحيث نجدهم بنفس جهة القاطع.
- ونجد أن واحدة منهم تتواجد بين أحد المستقيمين.
شاهد أيضًا : 10 طرق للمذاكرة الفعالة والناجحة
لقد أوضحنا في هذا المقال كل ما يخص أنواع الزوايا وقياسها، من حيث تعريفها وأنواعها.
كما أوضحنا عدة أمثلة لكي تسهل علينا معرفة الزوايا، وتناولنا أيضًا معرفة رسم الزوايا، وعرفنا المنقلة واستخداماتها، كما ذكرنا مسميات أخرى خاصة بالزوايا.
