قوانين الإحصاء والاحتمالات في الرياضيات
قوانين الإحصاء والاحتمالات في الرياضيات علم الإحصاء هو أحد فروع علم الرياضيات، ويهتم علم الإحصاء بجمع وتمثيل وإيجاد الاستنتاجات والقيام بتلخيصها من خلال مجموعة من البيانات المتوفرة
قوانين الإحصاء والاحتمالات
- نظرية الاحتمالات (Probability Theory)، هي تلك النظرية التي تهتم بالتجارب العشوائية التي يمكن أن يتم توقع نتائجها قبل حدوثها، ولكن لا يمكن أن يتم تأكيد نتائج أي تجربة مسبقًا قبل حدوثها بالفعل.
شاهد أيضًا: كيف تصبح عالمًا في الرياضيات
على سبيل المثال
- عند إلقاء قطعة من النقود مرة واحدة، فإنه يمكن توقع الناتج، إذ أنه سيكون إما صورة أو كتابة (ص أو ك)، لكن بالرغم من ذلك لا يمكن التأكيد على أي من الخيارين سوف يظهر في النتيجة.
- بينما الفضاء العيني هو جميع النتائج الممكن حدوثها والنتائج المقترحة لهذه التجربة العشوائية، ورمز الفضاء العيني هو (أوميجا).
أمثلة الفضاء العيني
بعض الأمثلة التي توضح كيفية إيجاد الفضاء العيني كما يلي:
مثال (1)
- أوجد الفضاء العيني لتجربة إلقاء قطعة نقود مرة واحدة.
الحل
- النتائج التي يمكن حدوثها عند رمي قطعة نقود واحدة هي إما صورة أو كتابة، وبالتالي فإن الفضاء العيني لهذه التجربة= (ص، ك).
مثال (2)
- أوجد الفضاء العيني لتجربة إلقاء حجر نرد مرة واحدة.
الحل
- النتائج التي يمكن حدوثها عند إلقاء حجر النرد هي إما 1، أو ،2، أو 3، أو 4، أو 5، أو 6
- بالتالي أن الفضاء العيني لهذه التجربة=
(1, 2, 3, 4, 5, 6).
مثال (3)
- أكتب الفضاء العيني لتجربة إلقاء قطعتين من النقود مرة واحدة
الحل
- النتائج التي يمكن حدوثها عند رمي قطعتين من النقود هي إما صورة مع صورة، أو صورة مع كتابة، أو كتابة مع كتابة، أو كتابة مع صورة، و
- بالتالي فإن الفضاء العيني لهذه التجربة= ((ص،ص)، (ص،ك)، (ك،ك)، (ك،ص)).
مثال (4)
- في تجربة عشوائية تم اختيار أسرة مكونة من طفلين فقط، وتم تدوين الطفلين بالسجلات حسب الجنس وتسلسل الميلاد، اكتب الفضاء العيني لهذه التجربة
الحل
- الفضاء العيني لهذه التجربة= ((ولد،ولد)، (ولد،بنت)، (بنت،بنت)، (بنت،ولد)).
مثال (5)
- أوجد الفضاء العيني لتجربة إلقاء قطعة نقد ثم حجر نرد.
الحل
- الفضاء العيني لتجربة إلقاء قطعة نقدية ثم حجر نرد= ((ص،1)، (ص،2)، (ص،3)، (ص،4)، (ص،5)، (ص،6) (ك،1)، (ك،2) (ك،3)، (ك،4)، (ك،5)، (ك،6)).
الحادث
والحادث هو عبارة عن مجموعة جزئية من الفضاء العيني (الأوميجا)، ويرمز له بالحرف ح، وهو أول حرف من كلمة حادث، وهناك عدة أنواع من الحوادث وهي كما يلي:
الحادث البسيط
- والحادث البسيط هو عبارة عن الحادث الذي فيه عنصر واحد من عناصر الأوميجا.
الحادث المركب
- والحادث المركب هو عبارة عن الحادث الذي فيه عنصرين أو أكثر من عناصر الأوميجا.
الحادث الأكيد
- والحادث الأكيد هو عبارة عن الحادث الذي فيه جميع عناصر الأوميجا دون نقصان أي عنصر.
الحادث المستحيل
- والحادث المستحيل هو الحادث الذي لا يوجد فيه أي عنصر من عناصر الأوميجا.
شاهد أيضًا: كيف تصبح ذكيًا بالرياضيات
أمثلة عناصر الحادث
بعض الأمثلة التي توضح كيفية إيجاد الحادث ونوعه كما يلي:
مثال (1)
في تجربة إلقاء حجر نرد مرة واحدة، أوجد كل ما يلي:
(1) عناصر الأوميجا
الحل
- الفضاء العيني= (1, 2, 3, 4, 5, 6).
(2) حادث ظهور عدد زوجي
الحل
- ح1= (2, 4 ,6). وهو يعتبر حادثًا مركبًا
(3) حادث ظهور عدد يقبل القسمة على 3
الحل
- ح2= (3,6)، ويعتبر حادثًا مركبًا.
(4) حادث ظهور عدد يقسم على 12
الحل
- ح3= ( ). وهي مجموعة فارغة أي خالية من أي عناصر أوميجا، ونوعه هو حادث مستحيل.
(5) ظهور عدد أقل أو يساوي 3
الحل
- ح4= (3,2,1)، أما نوعه فهو حادث مركب.
- (6) ظهور عدد أكبر أو يساوي 1 وأقل من 7.
- ح5= (1 ,4,3,2 ,5, 6)، أما نوعه فهو حادث أكيد.
احتمال وقوع الحادث
احتمال وقوع الحادث (ح)، هو عدد عناصر الحادث ح مقسومًا على عدد عناصر أوميجا.
أمثلة على احتمال الحوادث
بعض الأمثلة على كيفية إيجاد احتمال الحادث كما يلي:
مثال (1)
- شعبة من شعب الصف الثاني عدد طلابها الكلي 33 طالبًا، 13 طالبًا (من ذكور)، و20 طالبة (من الإناث)، فإذا تغيب أحد الطلاب، فما احتمال أن يكون من الذكور؟
الحل
- احتمال الحادث= عدد عناصر الحادث على عدد عناصر الفضاء العيني.
- واحتمال أن يكون الغائب من الذكور= عدد عناصر الذكور على عدد عناصر الصف بالكامل.
- احتمال أن يكون الغائب من الذكور= 33 /13.
مثال(2)
- في تجربة رمي حجر نرد مرة واحدة، ما احتمال ظهور العدد 5، وظهور عدد أكبر من 3.
الحل
- احتمال ظهور العدد 5 يساوي عدد عناصر ح1 على عدد عناصر الأوميجا. ل(ح1)=⅙،
- أما احتمال ظهور عدد أكبر من 3 تساوي عدد عناصر ح2 على عدد عناصر الأوميجا.
- ل(ح2) =6 /3.
- إذًا: ل(ح2) =½ أو 0.5 (الجواب بأبسط صورة ممكنة).
قوانين الاحتمالات
توجد بعض العمليات التي يمكن القيام بها على الحوادث مثل التقاطع، والاتحاد، والطرح، مما يساعد على ظهور حوادث جديدة تنتج من هذه العمليات، والقوانين ما يلي:
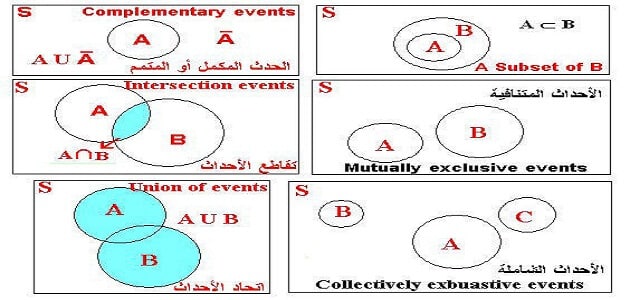
التقاطع (ح1∩ح2)
- يعني التقاطع وقوع الحادثين معًا، أو بمعنى آخر فإن تقاطع الحادثين هو عبارة عن العناصر المشتركة بينهما.
الاتحاد (حU1ح2)
- يعني الاتحاد وقوع أحد الحادثين على الأقل، أو بمعنى آخر فإن الاتحاد هو جمع عناصر الحادث الأول وعناصر الحادث الثاني.
الطرح (ح1-ح2)
- يعني الطرح وقوع الحادث الأول وعدم وقوع الحادث الثاني، أي كتابة عناصر الحادث الأول وعدم كتابة عناصر الحادث الثاني.
الحوادث المنفصلة (ح1∩ح2= فاي)
- الحوادث المنفصلة هو وقوع كل حادث على حدة ولا يمكن أن يقعا معًا، أي أن الحادثين منفصلين.
مجموع احتمالات حوادث التجربة = 1
- مجموع احتمالات الحوادث البسيطة التي تكون الفضاء العيني لأي تجربة عشوائية تساوي واحد. بعض خواص الاحتمالات
إذا كان أوميجا فضاءًا عينيًا لتجربة معينة، وكان ح1، ح2 حادثين في الفضاء العيني فإنه ينطبق عليها ما يلي:
- إذا كانت ح1 مجموعة جزئية من ح2، فإن
ل(ح1) أقل من أو تساوي ل(ح2).
- تقع قيمة احتمال أي حادث من الصفر للواحد، حيث أنه لا يمكن أن يكون الاحتمال قيمة سالبة، أو أكبر من واحد.
- ل(فاي) تساوي صفر، لأن (فاي) مجموعة خالية من العناصر، وعند قسمتها على عناصر الفضاء العيني فإن ناتج القسمة بالتأكيد يكون صفر.
- ل(ح1-ح2) =ل(ح1) -(ح1 ∩ح2).
أمثلة على قوانين الاحتمالات
هكذا بعض الأمثلة على إيجاد الاحتمالات كما يلي:
مثال(1)
- إذا كانت الحوادث التالية (ح1، ح2، ح3) هي حوادث بسيطة تكون الفضاء العيني لإحدى التجارب العشوائية، فإذا كانت ل(ح1) =0.25، ل(ح2) =0.35، أوجد قيمة ل(ح3).
الحل
- بما أن الحوادث الثلاثة هي مجموعة جزئية مكونة للأوميجا
- إذًا
- ل(ح1) + ل(ح2) +ل(ح3) = 1. 0.25+ 0.35+ ل(ح3) =1. 0.60+ ل(ح3) =1،
- وبطرح العدد 0.60 من الطرفين
- يصبح الناتج: ل(ح3) = 0.40
مثال (2)
- صندوق يحتوي على خمسة بطاقات مرقمة من 1 إلى خمسة، إذا تم سحت بطاقة واحدة عشوائية من الصندوق وتم تسجيل النتيجة، أوجد عناصر كل من الحوادث التالية
ح1: ظهور بطاقة تحمل عدد أكبر أو يساوي
الحل
ح1=(4,5).
ح2 ظهور بطاقة تحمل عدد أقل من 3.
الحل
- ح2=(1,2).
_ ح1 ∩ح2
الحل
- لا يوجد عناصر مشتركة بينالحادثين
ح1 ∩ح2= فاي.
_ (حU1ح2)
الحل
- ح1 اتحاد ح2 تعني وقوع أحدهما على الأقل، إذن (حU1ح2) =(1,2,4,5).
شاهد أيضًا: كيف أذاكر الرياضيات بسهولة
هكذا ومن هنا نكون ختمنا معكم اليوم مقالنا اليوم عن قوانين الإحصاء والاحتمالات في الرياضيات ونرجو أن يكون المقال قد نال على إعجابكم، إذا المقال حاز تقديركم ننتظر لايك وشير للمقال.
