ما هو قانون شبه المكعب
ما هو قانون شبه المكعب تحيط بالإنسان الكثير من الأشياء التي تمثل أشكالًا هندسية، منها ما هو مسطح الشكل يسمى ثنائي الأبعاد، مثل: المثلث والمربع والدائرة والمعين والمستطيل ومتوازي الأضلاع.
ومنها ما هو على شكل مجسم ويسمى ثلاثي الأبعاد، أي يأخذ حيز في الفراغ، وهو ذو ثلاثة أبعاد، مثل: الكرة، والمكعب والاسطوانة والمخروط وغيرهم.
ما هو قانون شبه المكعب
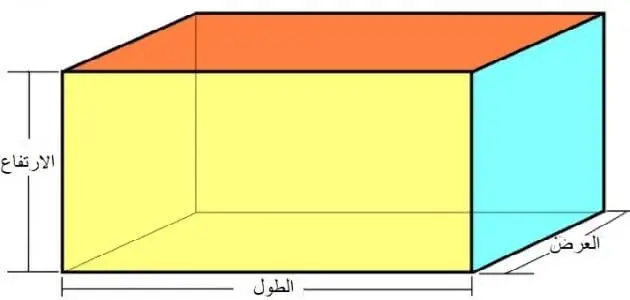
المكعب (Cube)، هو أحد المجسمات الهندسية ذات الأبعاد الثلاثية، وأبعاده هي (الطول، والعرض، والارتفاع).
حيث يتكون المكعب من ستة أوجه تتساوى في المساحة والحجم، كما يمثل كل وجه من أوجه المكعب شكلًا مربعًا، وحيث أن جميع أضلاع المربع تكون متطابقة، فإن:
طول المكعب=عرضه= ارتفاعه.
كما يتكون المكعب من 12 حرف، و8 رؤوس تنتج هذه الرؤوس عند التقاء ثلاثة أحرف مع بعضها البعض
ومن أمثلة الأشياء التي على شكل مكعب هي النرد العادي ذو الستة أوجه، أو الصندوق الذي يضم ستة أوجه مربعة.
شاهد أيضًا: أنواع المثلثات حسب الزوايا
شبه المكعب
- يطلق على شبه المكعب أيضًا اسم (متوازي
المستطيلات). - شبه المكعب هو أحد المجسمات الثلاثية الأبعاد، وهي الطول والعرض والارتفاع
- يتكون شبه المكعب من ستة أوجه، يمثل كل وجه من الأوجه شكل مستطيل.
- حيث أن وجهان منهما هم قاعدتي شبه المكعب، أما الأربعة هم أوجه جانبية
- يتكون شبه المكعب من الأحرف، وهي الحواف (القطع المستقيمة).
- التي تتكون منها الأوجه، إذ تتلاقى هذه الحواف عند نقطة يطلق عليها رؤوس شبه المكعب.
- القطعة المستقيمة التي تصل بين كل رأسين غير متجاورين (متقابلين)، تسمى قطر شبه المكعب.
- من أمثلة الأشياء التي على شكل شبه مكعب هي حجر (لبنة) البناء، أو صندوق الحذاء، أو مكبر الصوت.
خصائص شبه المكعب
يختص شبه المكعب بمجموعة من الخصائص التي تميزه عن غيره من الأشكال الهندسية، ومن بعض هذه الخصائص ما يلي:
- يشبه المكعب هو مجسم ذا ثلاثة أبعاد.
- هكذا يحتوي شبه المكعب على ستة أوجه يمثل كل منها شكل مستطيل.
- كل جانبين متقابلين في شبه المكعب متطابقان بما فيهم القاعدتين.
- هكذا يختلف المكعب عن شبه المكعب من حيث
- أطوال الأضلاع، حيث تكون أوجه المكعب على شكل مربعات، بينما أوجه شبه المكعب تكون على شكل مستطيلات.
- هكذا جميع المكعبات هي أشباه مكعبات -إذ أن المكعب هو شبه مكعب جميع أوجهه متساوية في الطول.
- هكذا ليس جميع أشباه المكعبات مكعبات.
قانون مساحة شبه المكعب
- المكعب هو مجسم متعدد الأوجه، وكي يمكن حساب مساحته مثل باقي المجسمات.
- لابد من الانتباه إلى وجود أوجه جانبية وقاعدتين.
- وحيث أن عدد أوجه المكعب الكاملة هي ستة أوجه متضمنة القاعدتين.
- فبالتالي مساحة المجسم تساوي مجموع مساحات جميع أوجهه.
- وبناء على أن شبه المكعب تتطابق أوجهه المتقابلة، إذًا مساحة شبه المكعب =
- 2(مساحة الوجه الأول) + 2(مساحة الوجه الثاني) +2 (مساحة الوجه الثالث).
- هكذا إذًا: المساحة شبه المكعب الكلية =
- مساحة أوجهه الجانبية + مساحة القاعدتين
أما
- مساحة أوجه شبه المكعب الجانبية=
- محيط المستطيل (القاعدة) × ارتفاع شبه المكعب. حيث أن
- مساحة المستطيل= (ط) × (ع)
إذ أن
- (ط= الطول)
- (ع= العرض).
أما
- محيط المستطيل= 2× (ط +ع)
- أو (2×ط + 2×ع).
شاهد أيضًا: كيف نحسب المساحة والمحيط
أمثلة حساب مساحة شبه المكعب
هكذا بعض الأمثلة التي توضح كيفية إيجاد مساحة شبه المكعب، وهي كما يلي:
مثال (1 )
- أوجد المساحة الكلية لصندوق مكعب الشكل، إذا علمت أن فيه، طول القاعدة= 10 سم، وعرضه= 8 سم، وارتفاعه 13سم.
الحل
أولًا: مساحة الأوجه الجانبية هي:
- محيط القاعدة× الارتفاع،
- بما أن القاعدة عبارة عن مستطيل فإن:
- المساحة الجانبية = محيط المستطيل × الارتفاع. المساحة الجانبية = 2× (ط +ع) ×الارتفاع.
- والمساحة الجانبية = 2×(10+8) ×13.
- المساحة الجانبية = 2×18×13.
- المساحة الجانبية =468 سم².
ثانيًا: مساحة شبه المكعب الكلية هي:
- المساحة الجانبية +مساحة القاعدتين.
- ومساحة شبه المكعب الكلية= 468 + 2(10× 8). مساحة شبه المكعب الكلية= 468+ 160.
- هكذا مساحة شبه المكعب الكلية= 628 سم².
مثال (2 )
- هكذا أوجد المساحة الكلية لشبه مكعب إذا علمت أن فيه طول القاعدة= 4 م وعرضها= 5 م، وارتفاعها 10م.
الحل
أولًا: مساحة الأوجه الجانبية، وهي:
- محيط القاعدة ×الارتفاع،
- وبما أن القاعدة عبارة عن مستطيل، فإن:
- المساحة الجانبية = محيط المستطيل ×الارتفاع. المساحة الجانبية = 2×(ط+ع) ×الارتفاع.
- والمساحة الجانبية = 2×(4+5) ×10.
- المساحة الجانبية = 2×9×10.
- المساحة الجانبية = 180م².
ثانيًا: مساحة شبه المكعب الكلية وهي:
- المساحة الجانبية +مساحة القاعدتين.
- هكذا مساحة شبه المكعب الكلية= 180+ 2(4×5)، مساحة شبه المكعب الكلية= 180+40.
- مساحة شبه المكعب الكلية= 220 م².
مثال (3 )
- هكذا أوجد المساحة الكلية الخاصة بصندوق على شكل شبه مكعب.
- هكذا إذا علمت أن فيه، طول القاعدة=4 سم، وعرضها=4 سم، وارتفاعها 4 سم.
الحل
أولًا مساحة الأوجه الجانبية، وهي:
- محيط القاعدة × الارتفاع،
- وبما أن القاعدة عبارة عن مستطيل فإن:
- المساحة الجانبية = محيط المستطيل × الارتفاع، المساحة الجانبية = 2× (ط+ ع) ×الارتفاع.
- المساحة الجانبية = 2×(4+4) ×4.
- والمساحة الجانبية = 2×8×4
- المساحة الجانبية =64 م².
ثانيًا مساحة شبه المكعب الكلية وهي:
- المساحة الجانبية +مساحة القاعدتين.
- مساحة شبه المكعب الكلية= 64+ 2(4×4).
- ومساحة شبه المكعب الكلية= 64+ 32.
- مساحة شبه المكعب الكلية=96 م².
مثال (4 )
- هكذا شبه مكعب، طول قاعدته 5 م، وعرضه 4 م، أما ارتفاعه فيساوي 10 م، أوجد المساحة الكلية في شبه المكعب
الحل
- مساحة شبه المكعب الكلية=
- المساحة الجانبية+ مساحة القاعدتين.
- مساحة شبه المكعب الكلية =
- (محيط القاعدة× الارتفاع)+ 2(مساحة القاعدة الواحدة).
- مساحة شبه المكعب الكلية =
- (2(الطول +العرض)× الارتفاع)+ 2(الطول× العرض).
- مساحة شبه المكعب الكلية =
- (2 (5 + 4) × 10) + 2 (4 × 5).
- مساحة شبه المكعب الكلية =
- (2 (9) × 10) + 2 (20).
- هكذا مساحة شبه المكعب الكلية = (18× 10) + 40. مساحة شبه المكعب الكلية =180+40. المساحة مساحة شبه المكعب الكلية =220 م².
حجم شبه المكعب - هكذا يعد معرفة حجم شبه المكعب أمرًا شديد الأهمية.
- هكذا حيث تكون هناك الحاجة في معرفة كمية الماء التي تلزم لملء خزان ماء على شكل شبه مكعب.
- وغيرها من المسائل التي يطلب فيها معرفة حجم شبه المكعب ذي الثلاثة أبعاد.
- وحجم شبه المكعب هو عبارة عن حاصل ضرب طوله في عرضه في ارتفاعه
- حجم شبه المكعب= الطول × العرض× الارتفاع.
أمثلة حجم شبه المكعب
هكذا بعض الأمثلة على كيفية حساب حجم شبه المكعب:
مثال (1 )
- خزان ماء على شكل شبه مكعب، طول قاعدته تساوي 2 م.
- وعرضه يساوي 4 م، أما ارتفاعه فيساوي 5 م، أوجد كم يلزم من الماء لتعبئة الخزان
الحل
- حجم شبه المكعب=2×4×5.
- إذًا: حجم شبه المكعب= 40 م³.
- يلزم 40 م³ من الماء لتعبئة الخزان.
مثال (2 )
- علبة مجوهرات على شكل شبه مكعب، طول قاعدتها يساوي 10 سم.
- وعرضها 14 سم، أما ارتفاعها فيساوي 15 سم، احسب حجمها.
الحل
- حجم شبه المكعب= الطول ×العرض× الارتفاع.
- حجم علبة المجوهرات=10×14×15.
- إذًا: حجم علبة المجوهرات= 2100 سم³.
مثال (3 )
- كتاب على شكل شبه مكعب، طول قاعدته 3 سم، وعرضه 4 سم، أما ارتفاعه فيساوي 5 سم، أوجد كم يلزم من الصفحات لتعبئته.
الحل
- حجم شبه المكعب= 3 × 4× 5.
- هكذا إذًا حجم شبه المكعب= 60 سم³.
- هكذا يحتاج الكتاب المكعب= الطول ×العرض× الارتفاع إلى 60 سم³ من الصفحات لتعبئته.
مثال (4 )
هكذا فطيرة محشوة بالجبن على شكل شبه مكعب، طولها 10 سم، وعرضها 5 سم، أما ارتفاعها 2 سم، كم من الجبنة يلزم في حشو الفطيرة بالكامل.
الحل
- حجم شبه المكعب= الطول ×العرض× الارتفاع
- وحجم شبه المكعب=10×5× 2
- حجم شبه المكعب= 100سم³.
إذًا يلزم 100 سم³ من الجبن في حشو الفطيرة بالكامل.
شاهد أيضًا: كيف تصبح عالمًا في الرياضيات
هكذا ومن هنا عزيزي القارئ نكون ختمنا معكم اليوم مقالنا عن ما هو قانون شبه المكعب وذكرنا كل ما يخص تلك الموضوع.
هكذا نرجو أن تكون المعلومات التي قدمناها إليكم مفيدة، لا تنسوا لايك وشير للمقال لتعم الفائدة على الجميع.
