أنواع المثلثات حسب الزوايا

أنواع المثلثات حسب الزوايا يوجد في البيئة المحيطة بالإنسان الكثير من الأشكال الهندسية المختلفة، ولعل أشهرها المربع والمستطيل والدائرة والمكعب وأيضًا المثلث.

وغيرها الكثير إذ تستخدم في العديد من تطبيقات الحياة العلمية والعملية، سواء كانت تتعلق بعلم الرياضيات بشكل مباشر أو بالعلوم الأخرى.

تعريف المثلث

• المثلث أحد الأشكال الهندسية المنتشرة في الحياة اليومية للفرد، ينتج عند رسم قطع مستقيمة تصل بين ثلاث نقاط لا تقع على استقامة واحدة (الرؤوس)، فهو شكل مغلق يتكون من ثلاث أضلاع وثلاث زوايا.
• مجموعهم ْ180درجة، ولكن يختلف قياس زوايا كل مثلث حسب شكل هذا المثلث.

شاهد أيضًا: كيف نحسب المساحة والمحيط

أنواع المثلثات حسب الزوايا

هناك تصنيفان أنواع المثلثات حسب الزوايا يقسم تبعًا لهما وهما كالتالي:

أنواع المثلث تبعًا إلى طول أضلاعه

يصنف المثلث تبعًا إلى طول أضلاعه إلى ما يلي:

مثلث متساوي الأضلاع

• ( Equilateral triangle)، المثلث المتساوي الأضلاع، مثلث جميع أضلاعه متساوية في الطول، وكذلك جميع زواياه متساوية في القياس أيضًا، كل زاوية تساوي 60ْ.

مثلث متساوي الساقين

• (Isosceles triangle)، المثلث متساوي الساقين، مثلث له ضلعين متساويين، كذلك الزاويتان المقابلتان لهذين الضلعين متساويتين.

مثلث مختلف الأضلاع

• (Scalene triangle)، المثلث مختلف الأضلاع، هو مثلث أطوال أضلاعه مختلفة، وكذلك جميع زوايا هذا المثلث تكون مختلفة في القياس أيضًا.

أنواع المثلث تبعًا إلى قياس زواياه

يصنف المثلث تبعًا إلى قياس زواياه إلى ما يلي:

مثلث قائم الزاوية

• (Right angled triangle)، المثلث قائم الزاوية
• هو مثلث قياس إحدى زواياه 90°.

مثلث متساوي الزوايا

• (Equal angled triangle)، المثلث المتساوي الزوايا، جميع زواياه قياسها 60°.

مثلث مختلف الزوايا

• (Different angled triangle)، المثلث مختلف الزوايا هو مثلث قياس جميع زواياه مختلف، مجموع زواياه 180°.

أنواع المثلث تبعًا إلى نوع زواياه

يصنف المثلث تبعًا إلى نوع الزاوية الداخلية إلى ما يلي:

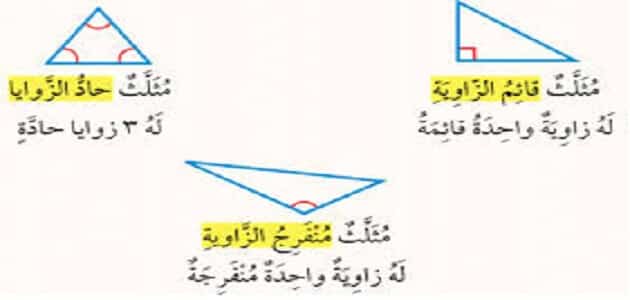
مثلث حاد الزوايا

• (acute triangle)، المثلث الحاد الزوايا هو مثلث يحتوي على ثلاثة زوايا، قياس كل منها أقل من °90 درجة.

مثلث قائم الزاوية

• (right triangle)، المثلث القائم الزاوية هو مثلث يحتوي على زاوية قائمة قياسها 90° درجة، والضلع المقابل للزاوية يسمى (الوتر)، وهو أطول أضلاع هذا المثلث.

مثلث منفرج الزاوية

• (obtuse triangle)، المثلث منفرج الزاوية هو مثلث قياس أحد زاوياه أكبر من 90 درجة.

شاهد أيضًا: مساحة المثلث ومحيطه وحجمه

قوانين المثلثات

هناك عدة قوانين خاصة بالمثلث، سواء المساحة أو المحيط، وغيرها وهي كما يلي:

 مساحة المثلث

• المساحة هي المنطقة الداخلية المحصورة التي تقع داخل حدود المثلث.

مساحة المثلث = حاصل ضرب طول نصف القاعدة في الارتفاع

• حيث أن ارتفاع المثلث هو العمود الساقط من إحدى الزوايا إلى الضلع المقابل والذي يطلق عليه القاعدة، أي أنه يصنع زاوية قائمة مع القاعدة.
• مساحة المثلث= ½ (القاعدة ×الارتفاع)

مثال

• مثلث متساوي الساقين طول ضلعه 6 سم وطول قاعدته 6 سم، وقيمة ارتفاعه 6 سم، ما مساحة المثلث؟

الحل

• مساحة المثلث=½×طول القاعدة ×الارتفاع

مساحة المثلث=½×6×6 مساحة المثلث=18 سم²

محيط المثلث

• محيط المثلث هو عبارة عن مجموع قياس حوافه.
• ومحيط المثلث يساوي مجموع قياس أطوال الأضلاع الثلاثة، على أن تكون وحدات القياس متساوية.
• محيط المثلث= طول الضلع الأول +طول الضلع الثاني+ طول الضلع الثالث

مثال

• مثلث أطوال أضلاعه 9 سم، 6 سم، 8 سم. أوجد محيطه.

الحل

• جمع هذه الأطوال.

محيط المثلث= 9 + 6 + 8 = 23 سم.

تطابق المثلثات

التطابق هو تساوي ضلع وزوايا أحد المضلعات مع نظيره من المضلع الآخر، إذ يتطابق المثلثين إذا تساوى أطوال أضلاعهما المتناظرة، وتساوى قياسات زواياهما المتناظرة أيضًا.

هناك بعض الحالات التي توضح إذا كان هناك تطابق وهي كالتالي:

 (ضلع، ضلع، ضلع)

• هكذا يقصد بها أن المثلثين متطابقان، إذا كان لهما ثلاثة أضلاع متماثلة، ومتساوية في القياس.

 (ضلع، زاوية، ضلع)

• هكذا يقصد بها أن المثلثين متطابقان، إذا تساوى فيهما طول ضلعين وزاوية محصورة بينهما، ويشترط أن تكون محصورة.

(زاوية، زاوية، ضلع)

• هكذا يقصد بها أن المثلثين متطابقان، إذا تساوى طول ضلع وزاويتين في المثلث الأول، مع طول ضلع وزاويتين متناظرتين في المثلث الثاني.

تشابه المثلثات

هكذا يكون المثلثين متشابهين، عندما تتساوى فيهما قياسات الزوايا المماثلة لبعضها، أي أن كل مثلثين متطابقين يكونا متشابهين، والعكس غير صحيح، وهناك بعض الحالات التي تبين إذا كان هناك تشابه بين المثلثين وهي كالتالي:

• إذا كان المثلثين متطابقين، فانهما بالتالي متشابهين
• وإذا كانت أطوال أضلاع المثلثين المتناظرة متساوية فإن المثلثين متشابهين.
• هكذا إذا كانت قياسات زوايا المثلثين المتناظرة متساوية، فإن المثلثين متشابهين.

متوسط المثلث

• متوسط المثلث (Median)، هو (الخط المستقيم الذي يصل بين أحد رؤوس المثلث ومنتصف الضلع المقابل له)
• هكذا مركز المثلث، هو نقطة تقاطع المتوسطات الثلاثة للمثلث، حيث إن مركز المثلث يقسم متوسط المثلث بنسبة 2:1

على سبيل المثال

إذا كان هناك مثلث أ ب ج، حيث إن أ د، ب س، ج ر متوسطات المثلث والنقاط د س ر منصفات أضلاع، والنقطة م مركز المثلث، فإن طول أ م مثلًا طول م د وطول ب م مثلًا م س، وهكذا، وبمعنى آخر إذا كان طول أ م يساوي6 سم، فإن طول م د يساوي 3 سم.

نظرية فيثاغورس

• هكذا نظرية فيثاغورس (phythagorth theory)، هي نظرية معروفة، وضعها العالم اليوناني الشهير فيثاغورس، إذ تستخدم فقط في المثلث قائم الزاوية.
• ( أن مساحة المربع الذي ينشأ على الوتر يساوي مساحة المربعين الواقعين على ضلعي القائمة)
• هكذا أي أن مربع طول الوتر=مربع ضلع القائمة الأول +مربع ضلع القائمة الثاني.

فإذا كان المثلث أ ب ج مثلث قائم الزاوية في ب فإن العلاقة بين أطوال الأضلاع هي:

• (أ ج)^2 = (أ ب) ^2 + (أ ج) ^2.

شاهد أيضًا: ما محيط المربع ومساحته

مثال

• مثلث قائم الزاوية، طول الضلع الأول يساوي 12، وطول الضلع الثاني يساوي 5. أوجد وتر المثلث.

الحل

• تربيع طولي الضلعين، 144 و25
• تطبيق قانون فيثاغورس
• الوتر 2 = 144 + 25 = 169
• أخذ جذر الناتج، فإنَ طول الوتر يساوي 13.
  أمثلة على أنواع المثلثات

بعض الأمثلة التي توضح أنواع المثلثات المختلفة:

مثال

صنف المثلثات الآتية حسب معطيات كل منها:

(1) مثلث قياس زواياه الداخلية:

(30°, 70°, 80°).

الحل

• مثلث حاد الزوايا، وذلك لأن قياس كل زاوية داخلية أقل من 90°، وبالتالي هو مثلث مختلف الأضلاع.

(2) مثلث قياس أطوال أضلاعه الثلاث:

(6 سم، 3 سم، 5 سم).

الحل

• مثلث مختلف الأضلاع، وذلك لأن طول كل ضلع يختلف عن طول الضلع الآخر، وبالتالي هو مثلث مختلف الزوايا.

(3) مثلث قياس زواياه الداخلية:

(90°, 50°, 40°).

الحل

• مثلث قائم الزاوية، وذلك لاحتوائه على زاوية قياسها 90°، وهو أيضًا مختلف الأضلاع.

(4) مثلث قياس زواياه الداخلية:

• (102°, 48°, 30°).

الحل

• مثلث منفرج الزاوية، وذلك لاحتوائه على زاوية قياسها أكبر من 90°، وهي زاوية (102)، وهو أيضًا مثلث مختلف الأضلاع.

(5) مثلث قياس أطوال أضلاعه الثلاث:

(2.5سم، 2.5سم، 4 سم).

الحل

• مثلث متساوي الساقين.

(6) مثلث قياس أطوال أضلاعه الثلاث:

(4م، 4م، 4م).

الحل

• مثلث متساوي الأضلاع، وكذلك هو مثلث متساوي الزوايا.

شاهد أيضًا: أنواع الزوايا وقياسها

حقائق عن المثلثات

هكذا بعض المعلومات الأساسية والحقائق عن المثلث هي كما يلي:

• المثلث ذو ستة عناصر، وهم ثلاثة أضلاع وثلاث زوايا.
• هكذا مجموع الزوايا الداخلية لأي مثلث تساوي مائة وثمانين درجة. (180°)
• مجموع طولي أي ضلعين دائمًا أكبر من طول الضلع الثالث في أي مثلث.
• هكذا عكس نظرية فيثاغورس صحيح، فإذا كان هناك مثلث فيه مربع الضلع الأكبر يساوي مجموع مربعي الضلعين الآخرين فبالتالي المثلث يكون قائم الزاوية.
• هكذا الزاوية الخارجية في المثلث تساوي مجموع الزاويتين الداخليتين البعيدتين، أي غير المجاورة لها.