كيف يحسب مساحة المعين
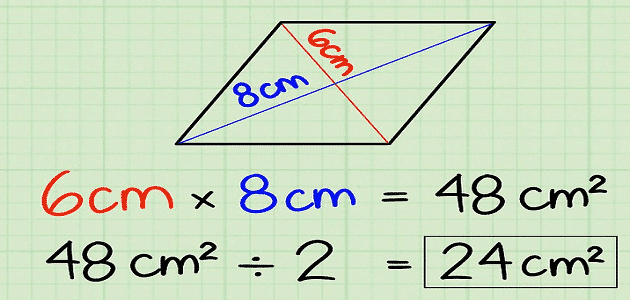
كيف يحسب مساحة المعين الهندسة الرياضية، هي فرع من فروع الرياضيات التي تهتم بدراسة الأشكال المختلفة، كما تهتم أيضًا بقياس الإحجام والمساحات لهذه الأشكال ومن هذه الأشكال الهندسية الرباعية (المعين).
الأشكال الرباعية
- الأشكال الرباعية، هي عبارة عن أشكال هندسية، ذات أربع أضلاع، وأربع رؤوس، وأربع زوايا، ولا يوجد رأس مشترك بين أي ضلعين متقابلين في الأشكال الرباعية.
- كما أن الرأسين المتقابلين في الأشكال الرباعية لا ينتميان إلى نفس الضلع، بينما الزاويتين المتقابلتين في الأشكال الرباعية يكون رأسيهما متقابلتين.
- يوجد في كل شكل رباعي قطران.
- الأشكال الرباعية تشمل المعين، ومتوازي الأضلاع، والمستطيل، والمربع، وشبه المنحرف.
شاهد أيضًا: ما محيط المربع ومساحته
المعين
- المعين (Rhombus)، ويتم نطقه بضم الميم، هو شكل رباعي الأضلاع، أطوال أضلاعه الأربعة متساوية، أو هو شكل رباعي يتكون من مثلثين ذوي ساقين متساويين، لهما قاعدة مشتركة.
- وهذه القاعدة المشتركة محذوفة، ويمتلك المعين جميع خصائص متوازي الأضلاع بالإضافة إلى عدد من الخصائص الأخرى الخاصة به.
صفات وخصائص المعين
المعين له عدد من الصفات، تتمثل كالتالي:
- جميع أضلاع المعين متساوية.
- كل ضلعين من أضلاع المعين متقابلين متوازيين.
- كل زاويتين من زوايا المعين متقابلتين متساويتين.
- المعين له قطران متعامدان، وينصف كل منهما الآخر.
- المعين له قطران، كل قطر ينصف زاويتين متقابلتين.
- يشكل القطران في المعين محوري تناظر له، وتشكل نقطة تقاطعهما مركز تناظر له أيضًا.
- كل قطر يقسم المعين إلى مثلثين كل منهما متساوي الساقين ومتطابقين.
- المعين له زاويتين حادتين وآخرتين منفرجتين ولكن إذا كانت إحدى زوايا المعين قائمة، عندئذٍ يكون الشكل مربعًا.
- والمعين هو حالة خاصة من متوازي الأضلاع.
- المعين بزاوية قائمة هو مربع.
- كل ضلع من أضلاع المعين يمكنه أن تشكيل مماسًا لدائرة واحدة.
مميزات المعين
يمكن أن يطلق على المضلع الرباعي البسيط أنه معين إذا تحقق أحد الشروط:
- إذا تساوت جميع أطوال أضلاع المضلع الرباعي.
- إذا تعامد القطران في المضلع الرباعي، ونصف كل منهما الآخر.
- وإذا نصف القطران في المضلع الرباعي كل زاوية داخلية.
- إذا كان المضلع الرباعي متوازي أضلاع، ونصف أحد قطريه إحدى زواياه.
- وإذا كان المضلع الرباعي متوازي أضلاع، وتساوى فيه ضلعان متجاوران.
- إذا كان المضلع الرباعي متوازي أضلاع، وتعامد قطراه.
مساحة المعين
مساحة المعين هي قياس المنطقة المحصورة التي تقع على سطح المعين، بمعنى قياس المنطقة التي تقع بين أضلع المعين الأربعة، ووحدة قياس مساحة المعين هي المتر المربع (م²)، أو السنتيمتر المربع (سم²).
كيف يحسب مساحة المعين
قانون طولي قطري المعين يتم في هذه الطريقة يمكن حساب مساحة المعين من خلال معرفة طولي قطريه، وتكون مساحة المعين تساوي نصف حاصل ضرب طولي قطريه، حسب القانون الآتي:
- مساحة المعين=حاصل ضرب القطرين÷2 مساحة المعين= (طول القطر الأول ×طول القطر الثاني) ÷2.
- مثال(1)، إذا علمت أن مساحة معين تساوي 45 سم²، وكان طول أحد قطريه يساوي 10 سم، فما طول قطره الثاني.
- الحل، مساحة المعين (طول القطر الأول ×طول القطر الثاني) ÷2، 45= (10×طول القطر الثاني) ÷2، (45×2) = (10×طول القطر الثاني)، طول القطر الثاني=(45×2) ÷10=90÷10=9 سم.
- مثال(2)، احسب مساحة معين طول قطره الأول يساوي 8 سم وطول قطره الثاني يساوي 4 سم.
- الحل، مساحة المعين= (طول القطر الأول ×طول القطر الثاني) ÷2 مساحة المعين=(8×4) ÷2= 32÷2=16 سم².
شاهد أيضًا: كيف يتم حساب مساحة مستطيل
قانون مساحة الحالات الخاصة للمعين
قانون مساحة متوازي الأضلاع
كيف يحسب مساحة المعين حيث إن المعين عبارة عن حالة خاصة من متوازي الأضلاع، فإنه يتم حساب مساحة المعين في هذه الحالة عن طريق قانون مساحة متوازي الأضلاع.
أي يتم استخدام ارتفاع المعين (المسافة العمودية بين أي ضلعين متقابلين)، وقاعدة المعين (أحد أحرف أو أضلاع المعين)، ويتم ذلك من خلال القانون الآتي:
- مساحة المعين=ارتفاع المعين ×طول قاعدة المعين.
- مثال (1)، أوجد ارتفاع معين إذا علمت أن مساحته تساوي 80 سم²، وطول ضلعه يساوي 10سم.
- الحل، مساحة المعين=ارتفاع المعين ×طول قاعدة المعين، 80=ارتفاع المعين×10، ارتفاع المعين=80÷ 10= 8 سم.
- مثال(2)، احسب مساحة قطعة بلاستيكية على شكل معين إذا علمت أن ارتفاعها يساوي 10 سم وطول أحد أضلاعها يساوي 8 سم.
- الحل، قانون مساحة المعين بدلالة الارتفاع وطول جانبه= الارتفاع ×طول الضلع.
- يتم تعويض قيمة الارتفاع وطول الضلع بالقانون. مساحة القطعة = 10 سم 8 سم.
- إذن مساحة القطعة البلاستيكية =80 سم².
قانون حساب المثلثات
حيث تستخدم في هذه الطريقة حساب المثلثات، وذلك من أجل حساب مساحة المعين، بحيث أن مساحة المعين يساوي مربع طول ضلع المعين مضروبًا في (جا) إحدى زواياه حسب القانون الآتي:
- مساحة المعين= (طول ضلع المعين)2×جا إحدى زوايا المعين.
- مثال، أوجد مساحة معين إذا علمت أن طول ضلعه يساوي 4 سم، وقياس إحدى زواياه تساوي 30 درجة.
- الحل، مساحة المعين= (طول ضلع المعين)2×جا إحدى زوايا المعين مساحة المعين=(4)2×جا30.
- مساحة المعين=16×0.5= 8 سم².
الفرق بين المربع والمعين
المعين هو حالة خاصة من المربع إذ إن المعين ذو الزاوية القائمة هو مربع، ويختلف المعين عن المربع في الآتي:
- المربع زواياه وأضلاعه متساوية.
- زوايا المربع = 90ْ.
- أما المعين أضلاعه المعين، ولكن ليس من الضروري أن تكون الزوايا متساوية.
محيط المعين
محيط المعين هو طول الخط الذي يحيط بأي شكل ثنائي الأبعاد، مثل: المعين، والدائرة، والمستطيل، والدائرة، ووحدة قياس محيط المعين هي السنتيمتر (سم)، أو المتر (م)، وبما أن الأربع أضلاع في المعين متساوية.
فإن محيط المعين يساوي مجموع أضلاعه الأربعة أو 4×طول الضلع الواحد، محيط المعين= مجموع أضلاعه أو محيط المعين= 4× طول الضلع كما في الأمثلة الآتية:
- مثال(١)، احسب محيط معين طول ضلعه 6 سم.
- الحل، محيط المعين يساوي 4× طول الضلع، محيط المعين= 4× 6=24 سم.
- مثال(2)، احسب طول ضلع المعين الذي محيطه يساوي 32 سم.
- الحل، بتطبيق القانون، محيط المربع =4× طول الضلع 32=4×طول الضلع.
- طول الضلع =32÷4=8 سم، إذًا؛ طول ضلع المعين يساوي 8 سم.
- مثال (3)، مزرعة على شكل معين، طول أحد جوانبها يساوي 60 م، أراد صاحبها إحاطتها بسياج، فكم مترًا من السياج يلزم لإحاطة المزرعة.
- الحل، محيط المعين= 4 × طول الضلع.
- نعوض قيمة طول الضلع بالقانون.
- محيط المزرعة= 4× 60 =240 متر
- إذًا يلزم 240 مترًا من السياج لإحاطة المزرعة.
خطوات رسم معين
إذا علم طول قطريين المعين يمكن رسمه بأسلوب مبسط، وبشكل دقيق كما يلي:
- خطوات رسم معين إذا علم أن طول قطره الأول 6 سم، وطول قطره الثاني 8 سم.
- الخطوة الأولى، يتم رسم قطعة مستقيمة مقدارها 6 سم باستخدام المسطرة، وتسمى القطعة أب، حيث تمثل هذه القطعة المستقيمة طول القطر الأول.
- والخطوة الثانية، يتم تعيين نقطة المنتصف للقطعة أب، ونسميها بالنقطة م.
- الخطوة الثالثة، يتم تحديد طول نصف القطر الثاني باستخدام المسطرة، وهو (8 ÷ 2) فيصبح الطول يساوي 4 سم.
- والخطوة الرابعة، يتم رسم القطعة المستقيمة التي طولها 4 سم بشكل عمودي على النقطة م، وذلك باستخدام المثلث قائم الزاوية، حيث يتم تسمية هذه القطعة ج م.
- الخطوة الخامسة، يتم رسم قطعة مستقيمة من الجهة الأخرى طولها 4 سم أيضًا عمودية على النقطة م، وذلك بالطريقة نفسها، حيث يتم تسمية هذه القطعة د م.
- الخطوة السادسة، يتم توصيل خط مستقيم بين النقاط أ ب ج د، وعندها يتشكل المعين أ ب ج د.
شاهد أيضًا: كيف نحسب المساحة والمحيط
ونكون بهذا أنجزنا مقالنا اليوم عن كيف يحسب مساحة المعين ونرجو أن تكون المعلومات المقدمة مفيدة ليكم، لا تنسوا لايك وشير للمقال، لتعم الاستفادة على جميع المتابعين.
