ما هي طريقة إيجاد المضاعف المشترك الأصغر

بواسطة ليلى جبريل أخر تحديث فبراير 28, 2022

ما هي طريقة إيجاد المضاعف المشترك الأصغر الجبر هو أحد فروع علم الرياضيات الهامة، وقد عرف بهذا الاسم (الجبر) نسبة إلى عالم الرياضيات المسلم الشهير محمد بن موسى الخوارزمي، صاحب كتاب (المختصر في حساب الجبر والمقابلة)، وكلمة (الجبر) أصلها يرجع إلى اللغة العربية.

وتعني فرع علم الرياضيات الذي يقوم بإحلال الرموز مكان الأعداد المعلومة أو المجهولة.

المضاعف المشترك الأصغر

المضاعف المشترك الأصغر للأعداد الطبيعية، هو أصغر عدد يقبل القسمة على هذه الأعداد بدون وجود أي باقٍ لهذه الأعداد.

أي هو عبارة عن مضاعفة كل عدد حتى الوصول إلى أصغر مضاعف مشترك بين هذه الأعداد (عددين أو أكثر)، وهو يكون دائمًا موجب، ويرمز له ب (م.م.أ)

حيث أن:

(م): مضاعف
و(م): مشترك
(أ): أصغر
والرمز عبارة عن الأحرف الأولى للكلمات الثلاثة.
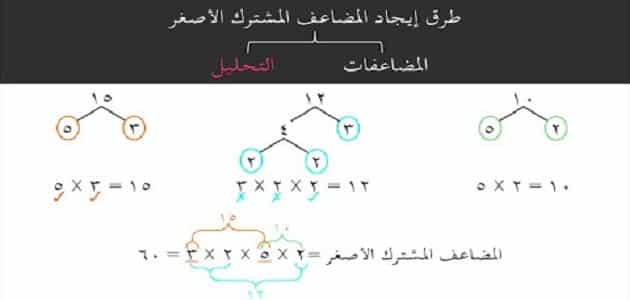
طرق إيجاد المضاعف المشترك الأصغر للأعداد إيجاد المضاعف المشترك الأصغر للأعداد الطبيعية يمكن أن يتم بطريقتين:

شاهد أيضًا: ما هي خصائص الأعداد الحقيقية

الطريقة الأولى

أن يتم كتابة مضاعفات العدد من خلال ضرب العدد المعطى في العدد واحد، ثم ضربه في العدد اثنين، ثم ضربه في العدد ثلاثة، ثم ضربه في العدد أربعة وهكذا……
لكن من سلبيات أنها تتطلب وقتًا أطول وجهدًا أكبر، حتى يتم الحصول على أصغر مضاعف مشترك مطلوب.

الطريقة الثانية

أن يتم استخدام التحليل إلى العوامل الأولية للعدد، ثم ضربها في بعضها البعض حسب تكرارها وهي طريقة أكثر سهولة والطريقتين صحيحتين تمامًا.

أمثلة المضاعف المشترك الأصغر للأعداد

بعض الأمثلة على كيفية إيجاد المضاعف المشترك الأصغر للأعداد، وهي كما يلي:

مثال(1)

أوجد المضاعف المشترك الأصغر (م.م.أ) للعددين 6،

الحل

أولًا: يتم إيجاد مضاعفات كل من العددين.

مضاعفات العدد 6 هي: 6، 12، 18، 24، 30، 36، 42، 48، 54، …….
مضاعفات العدد 9 هي: 9، 18، 27، 36، 45، 54، 63، 72، 81، 90 …………
ثانيًا: يتم البحث عن المضاعفات التي تشترك بين العددين وهو: 18، 36، …….
ثالثًا: يتم أخذ أصغر مضاعف من هذه المضاعفات وهو 18.
إذًا المضاعف المشترك الأصغر (م.م.أ) للعددين هو 18.

مثال(2)

أوجد المضاعف المشترك الأصغر (م.م.أ) للأعداد 3، 6، 9.

الحل

أولًا إيجاد مضاعفات كل عدد من هذه الأعداد.
مضاعفات العدد 3 هي: 3، 6، 9، 12، 15، 18،…..
ومضاعفات العدد 6 هي: 6، 12، 18، 24، 30، 36، 42، …………
مضاعفات العدد 9 هي: 9، 18، 27، 36، 45، 54، 63، 72، 81، 90 …………
ثانيًا: نبحث عن المضاعفات المشتركة بين العددين وهي: 9، ……
ثالثًا: يتم أخذ أصغر مضاعف من هذه المضاعفات وهو 9.
إذًا المضاعف المشترك الأصغر (م.م.أ) للعددين هو 9.

مثال(3)

أوجد المضاعف المشترك الأصغر (م.م.أ) للأعداد 45، 60، 30 باستخدام طريقة التحليل إلى العوامل الأولية

الحل

أولًا: يتم تحليل كل عدد من هذه الأعداد إلى عوامله الأولية كالآتي:

45=3×3×5
60=2×2×5×3
30=2×3×5

ثانيًا: يتم أخذ أكبر تكرار موجود في العوامل الأولية، يتم ملاحظة أن العامل 2 تكرر مرتين، والعامل 3 تكرر مرتين، أما العامل 5 فتكرر مرة واحدة، بهذا يكون المضاعف المشترك الأصغر هو حاصل ضرب تكرارات كل عامل من العوامل الأولية.
إذًا م.م.أ للأعداد 45، 60، 30 هو
2×2×3×3×5= 180

شاهد أيضًا: ما هي الأعداد الأولية في الرياضيات

مثال(4)

قام محمود ومجدي بالمشاركة في إحدى سباقات الجري الرياضية، فإذا علمت أن محمود احتاج إلى 4 دقائق لإكمال الدورة والوصول للنقطة التي بدأ منها.
أما مجدي فقد احتاج إلى 6 دقائق لإكمال الدورة والوصول إلى النقطة التي بدأ منها، فبعد كم دقيقة سيكمل كلاهما الدورة معًا وفي الوقت نفسه.

الحل

أولًا: إيجاد مضاعفات العددين 4، 6
مضاعفات العدد 4 هي: 4، 8، 12، 16، 20، 24، ……
مضاعفات العدد 6 هي: 6، 12، 18، 24، 30، 36، 42، 48…………
ثانيًا: إيجاد المضاعفات المشتركة بين العددين وهي: 12، 24، …..
ثالثًا: يتم أخذ أصغر مضاعف من هذه المضاعفات وهو 12.
إذًا يكملان الدورة كاملة معًا لأول مرة في الدقيقة 12 وهو يمثل المضاعف المشترك الأصغر.

مثال(5)

احسب المضاعف المشترك الأصغر (م.م.أ) للأعداد، 12، 6، 4.

الحل

اولًا: يتم حساب المضاعفات لكل عدد من الأعداد:

مضاعفات العدد 12 هي:12، 24، 36، 48، 60، 84.. وهكذا.
ومضاعفات العدد 6 هي: 6، 12، 18، 24، 30، 36، ……الخ
مضاعفات العدد 4 هي:4، 8، 12، 16، 20،….. وهكذا.
ثانيًا: يتم البحث عن العدد الأصغر المشترك لهما في المضاعفات:
وهو العدد 36.

المضاعف المشترك الأصغر للمقادير الجبرية

إيجاد المضاعف المشترك الأصغر للأعداد لا يقتصر على الأعداد الطبيعية فقط، بل يمكن أيضًا إيجاد المضاعف المشترك الأصغر للمقادير والحدود الجبرية الرياضية.
- ويمكن أن يعرف المضاعف المشترك الأصغر لمقدارين جبريين أو أكثر بأنه هو حاصل ضرب عوامل المقادير ببعضها البعض بدون تكرار الحد المتشابه فيما بينها.
طرق إيجاد المضاعف المشترك الأصغر للمقادير الجبرية
إيجاد المضاعف المشترك الأصغر للحدود أو المقادير الجبرية يمكن أن يتم من خلال تحليل كل منها إلى عوامله الأولية، وتحديد العوامل المشتركة بينهم، ثم القيام بضرب عوامل الحدود في بعضها البعض ولكن بدون إعادة كتابة الناتج المتشابه فيما بينهم.