بحث عن الأشكال الهندسية وخواصها

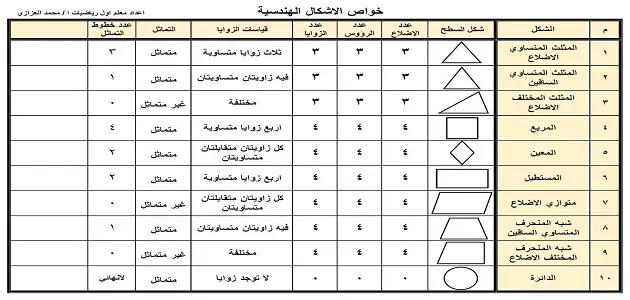
بحث عن الأشكال الهندسية وخواصها تتعدد الأشكال الهندسية، وتتنوع سواء في الشكل أو في الخواص، إذ تستخدم في الكثير من التطبيقات المختلفة في الحياة العملية، مما يضفي لمسات جميلة وجديدة سواء في تصميمات البناء والأثاث وغيرها من الاستخدامات.

ومن أمثلة الأشكال الهندسية المربع والدائرة، والمعين، وشبه المنحرف، والمستطيل وغيرها من الأشكال الهندسية.

الأشكال الهندسية وخواصها

• الأشكال الهندسية عبارة عن أشكال الجمادات المختلفة المحيطة بنا، وتتعدد أشكالها وأيضًا أبعادها، فهناك أشكالًا هندسية ثنائية الأبعاد، أو ثلاثية الأبعاد، وغيرها، وأبرز الأشكال الهندسية المثلث، والمربع، والمستطيل، والدائرة.

شاهد أيضًا: كيف يحسب مساحة المعين

الأشكال الهندسية ثنائية الأبعاد

• والأشكال الهندسية ثنائية الأبعاد هي عبارة عن أسطح مستوية لها طول وعرض مثل: المضلعات الرباعية، والمضلعات الخماسية، والمضلعات السداسية.

الأشكال الهندسية ثلاثية الأبعاد

• والأشكال الهندسية ثلاثية الأبعاد هي عبارة عن أسطح مستوية لها طول وعرض وارتفاع مثل: الأسطوانة، والمكعب، والهرم، والمخروط، والكرة.

الأشكال الهندسية الرباعية

• والأشكال الهندسية رباعية الأبعاد هي عبارة عن مضلع يتكون من 4 أضلاع و4 زوايا و4 رؤوس، مثل المستطيل، والمربع، والمعين، ومتوازي الأضلاع، وشبه المنحرف.

أمثلة على الأشكال الهندسية وخواصها

المستطيل

يمتلك المستطيل (Rectangle) عدة خصائص تميزه وهي كالتالي:

1. المستطيل هو عبارة عن متوازي أضلاع.
2. كل ضلعين متقابلين متوازيين ومتساويين في الطول.
3. المستطيل له قطران متساويان في الطول وينصف كل منهما الآخر.
4. كل زوايا المستطيل قائمة.
5. مساحة المستطيل = الطول × العرض.
6. محيط المستطيل = 2×(الطول + العرض)،أو مجموع أضلاعه الأربعة.

المثلث

والمثلث (Triangle)، عبارة عن شكل هندسي له عدة خصائص كالآتي:

• المثلث له ثلاثة أضلاع.
• مجموع زوايا المثلث تساوي 180 درجة.

ينقسم المثلث حسب قياس زواياه إلى ثلاثة أنواع، وهي:

• المثلث قائم الزاوية الذي يمتلك زاوية تساوي 90 درجة.
• المثلث حاد الزاوية قياس زاويته أقل من 90 درجة المثلث منفرج الزاوية قياس زاويته أكثر من 90 درجة وأقل من 180 درجة.
• مساحة المثلث = 1/2 × طول القاعدة × الارتفاع.

ينقسم إلى ثلاثة أنواع بناءًا على طول أضلاعه

• مثلث مختلف الأضلاع: هو مثلث يكون أطوال الأضلاع غير متساوية.
• ومثلث متساوي الساقين: هو المثلث الذي يكون طول ساقين فيه متساويين، ويكون قياس زاويتي قاعدته متساويًا.
• مثلث متساوي الأضلاع: هو مثلث أضلاعه متساوية الأطوال.

متوازي الأضلاع

متوازي الأضلاع(Parallelogram)، له العديد من الخصائص، ومنها ما يأتي:

• كل ضلعين متقابلين متوازيين.
• كل ضلعين متقابلين متساويين في الطول.
• قطرا متوازي الأضلاع ينصف كل منهما الآخر.
• مجموع كل زاويتين متتاليتين 180 درجة.
• كل زاويتين متقابلتين متساويتين في القياس.
• مساحة متوازي الأضلاع =طول القاعدة × الارتفاع.
• محيط متوازي الأضلاع =مجموع أطوال أضلاعه أو ضعف مجموع أي ضلعين متتاليين في متوازي الأضلاع.

شاهد أيضًا: ما محيط المربع ومساحته

المعين

والمعين (Rhombus)، هو أحد الأشكال الهندسية، له عدة خصائص، ومنها ما يأتي:

1. المعين عبارة عن متوازي أضلاع.
2. جميع أضلاع المعين متساوية في الطول.
3. كل ضلعين متقابلين متوازيين.
4. كل زاويتين متقابلتين متساويتين في القياس.
5. قطرا المعين متعامدان وينصف كل منهما الآخر.
6. مجموع كل زاويتين متتاليتين 180 درجة.
7. مساحة المعين = طول القاعدة × الارتفاع، أو 1/2 × (طول القطر الأول× طول القطر الثاني). _ محيط المعين = 4× طول الضلع، أو مجموع أطوال أضلاعه (لأنها متساوية).

المربع

المربع (Square)، شكل هندسي له عدد من الخصائص وهي كما يلي:

• والمربع عبارة عن متوازي أضلاع.
• جميع أضلاع المربع متساوية في الطول ومتعامدة على بعضها البعض.
• كل ضلعين متقابلين متوازيين.
• جميع زوايا المربع متساوية في القياس.
• قطرا المربع متعامدان ومتساويان في الطول وينصف كل منهما الآخر.
• المربع حالة خاصة من المستطيل، لأن فيه ضلعين متجاورين متطابقين مثل المستطيل.
• المربع حالة خاصة من المعين، لأن إحدى زواياه قائمة.
• محيط المربع = 4 × طول الضلع، أو مجموع أطوال أضلاعه الأربعة.
• مساحة المربع = طول الضلع × طول الضلع.

شبه المنحرف

شبه المنحرف (Trapezoid)، هو شكل هندسي رباعي الأبعاد، له عدة خصائص وهي كما يلي:

• وشبه المنحرف فيه ضلعان فقط متوازيان وهما قاعدتي شبه المنحرف.
• ارتفاع شبه المنحرف عبارة عن الخط العمودي الواصل بين القاعدتين، في حين أن الضلعين الآخرين غير متوازيين.
  • وهما يمثلان ساقي شبه المنحرف، فإذا تساوى الساقان في الطول يسمى شبه المنحرف (متساوي الساقين)، وبناءًا عليه فإن زوايا القاعدة متساوية في القياس، وقطر شبه المنحرف متطابقان في الطول.

المخروط

ينتج المخروط (Cone)، عن دوران مثلث قائم الزاوية دورة كاملة حول أحد ضلعي الزاوية القائمة، وله عدة خصائص كما يلي:

• قاعدة المخروط دائرية الشكل.
• النقطة الواقعة أعلى المخروط تسمى رأس المخروط.
• المستقيم العمودي الواصل بين مركز قاعدة المخروط ورأسه يسمى ارتفاع المخروط.

يمكن حساب مساحة المخروط الكلية عن طريق حساب مساحة قاعدة المخروط بالإضافة إلى المساحة الجانبية للمخروط وجمعهما سويًا كما يلي:

• مساحة قاعدة المخروط = π ×نق².
• مساحة القطاع الدائري (المساحة الجانبية للمخروط) = π×نق× ل.
• بالتالي فإن المساحة الكلية للمخروط =π × نق (ل + نق).
• حيث إن (ل) طول راسم المخروط.
• (نق) نصف قطر قاعدة المخروط.
• يتم حساب حجم المخروط من خلال القانون الآتي: 1/3 π × نق² × ع.
• حيث إن (نق) نصف قطر قاعدة المخروط.
• (ع) ارتفاع المخروط.

الدائرة

تتشكل الدائرة (Circle)، من رسم منحنى حول نقطة مركزية، لها عدد من الخصائص كما يلي:

1. جميع نقاط المنحنى المكون للدائرة تبعد مسافة ثابتة عن المركز، ويسمى نصف القطر (نق).
2. قطر الدائرة عبارة عن قطعة مستقيمة تصل بين أي نقطتين على المحيط وتمر بالمركز، يساوي ضعفي نصف القطر.
3. الوتر هو القطعة الواصلة بين أي نقطتين من الدائرة.
4. الزاوية المركزية للدائرة: هي الزاوية التي يقع رأسها في مركز الدائرة، وضلعاها نصفا قطرين في الدائرة.
5. الزاوية المحيطية هي الزاوية التي يقع رأسها على الدائرة، وضلعاها وتران في الدائرة.
6. طول المنحنى المشكل للدائرة يمثل محيطها.
7. وعند قسمة قيمة محيط الدائرة على قطرها تنتج النسبة التقريبية وتساوي 3.14159 وتسمى (π) الدائرة = 2 × π × نصف القطر.
8. مساحة الدائرة = (نصف القطر)2 × π.

الأسطوانة

الأسطوانة (Cylinder)، شكل من الأشكال الهندسية لها عدة خصائص وهي كما يلي:

• والاسطوانة لها قاعدتان مسطحتان على شكل دائري.
• الاسطوانة لها واجهة واحدة، تنتج من دوران مستطيل حول أحد أضلاعه.

المكعب

المكعب (Cube)، شكل من الأشكال الهندسية يتميز بعدد من الخصائص وهي كما يلي:

• والمكعب له 6 أوجه متماثلة الشكل ومتساوية الأطوال.
• في المكعب كل وجه له 4 أضلاع ويكون على شكل مربع.
• المكعب له 12 حرف و8 رؤوس.

الهرم الثلاثي

هكذا وهو شكل من الأشكال الهندسية، له عدة خصائص:

• له 4 أوجه، جميع أوجهه الجانبية مثلثة الشكل. _ قاعدة الهرم مثلثة الشكل.
• له 4 رؤوس و6 أضلاع.

الهرم الرباعي

وهو أحد الأشكال الهندسية، له عدة خصائص وهي كما يلي:

• الهرم الرباعي له 5 أوجه، جميع أوجهه الجانبية مثلثة الشكل.
• قاعدة الهرم الرباعي مربعة الشكل.
• الهرم الرباعي له 5 رؤوس و8 أضلاع.

الهرم الخماسي

هكذا أحد الأشكال الهندسية، له عدد من الخصائص وهي كما يلي:

• الهرم الخماسي له 6 أوجه.
• والهرم الخماسي جميع أوجهه الجانبية مثلثة الشكل. _ قاعدة الهرم الخماسي شكلها خماسي الأضلاع.
• الهرم الخماسي له 6 رؤوس و10 أضلاع.

شاهد أيضًا: كيف يتم حساب مساحة مستطيل

خاتمة بحث عن الأشكال الهندسية وخواصها

هكذا ونكون بهذا أنجزنا مقالنا اليوم عن بحث عن الأشكال الهندسية وخواصها ونرجو أن تكون المعلومات المقدمة مفيدة ليكم، لا تنسوا لايك وشير للمقال.