مساحة شبه المنحرف

مساحة شبه المنحرف الأشكال الهندسية كثيرة ومتنوعة تختلف في الشكل والأبعاد، وبالتالي تختلف في المساحة والحجم، منها أشكالًا ثنائية الأبعاد، ومنها مجسمات ذات بعد ثلاثي ومن أمثلتها المربع والمستطيل والمثلث، وشبه المنحرف وغيرها الكثير.

تعريف المضلع

المضلع هو شكل هندسي مغلق، يحتوي على ثلاثة قطع مستقيمة أو أكثر، إذ تتقاطع كل قطعتين من هذه القطع سويًا لتشكل نقطة التقاء تسمى رأس المضلع، ومن أمثلة المضلعات، المربع والمستطيل، ومتوازي الأضلاع وشبه المنحرف وغيرها من الأشكال الهندسية.

شاهد أيضًا: بحث عن الأشكال الهندسية وخواصها

المضلع الرباعي

• المضلع الرباعي هو شكل هندسي مغلق، يحتوي على أربعة أضلاع فقط، حيث أن مجموع أطوال الأضلاع سويًا يمثل محيط المضلع.
  • في حين أن أقطار المضلع الرباعي عبارة عن قطعة مستقيمة تصل كل زاويتين غير متجاورتين، إذ تجزي الشكل إلى جزأين كل منهما على شكل مثلث.
• وحيث أن مجموع قياس زوايا المثلث الواحد الداخلية تساوي 180 درجة، إذًا مجموع زوايا الشكل الرباعي تساوي 360 درجة.
  • ومن أمثلة الأشكال الهندسية التي تمثل مضلعات، المربع والمستطيل، وشبه المنحرف، ومتوازي الأضلاع، بينما المثلث لا ينتمي إلى قائمة المضلعات الرباعية الشكل لأنه ثلاثي الأضلاع.

شبه المنحرف

شبه المنحرف (Trapezoid)، هو من أهم الأشكال الهندسية الرباعية الأضلاع له عدد من الخصائص التي تميزه منها ما يلي:

• وشبه المنحرف شكل رباعي الأضلاع (أي التي تحتوي على أربعة جوانب).

• وشبه المنحرف فيه ضلعان فقط متوازيان، وهما يمثلان قاعدتي شبه المنحرف.
• ارتفاع شبه المنحرف، هو عبارة عن المسافة العمودية التي بين القاعدتين.
• ضلعان شبه المنحرف الآخران غير متوازيان، وهما يمثلان ساقي شبه المنحرف، فإذا تطابق الساقين يسمى شبه المنحرف متساوي الساقين، وبما أن الساقين متطابقين فإن زوايا القاعدة تكون متساوية أيضًا، ويكون قطري شبه المنحرف متطابقين أيضًا.

أنواع شبه المنحرف

هناك عدة أنواع من شبه المنحرف وهي كما يلي:

شبه منحرف عام

شبه المنحرف العام عبارة عن مضلع رباعي فيه:

• ضلعان متوازيان.
• قطران غير متساويين، ويتقابل القطران عند نقطة معينة.
• يمثل ارتفاع شبه المنحرف العام المسافة العمودية بين الضلعين المتوازيين.
• يحتوي شبه المنحرف العام على أربع زوايا غير متساوية، ولكن مجموعها يساوي 360 درجة، كل زاويتين محصورتين بين الضلعين المتوازيين مجموعهما يساوي 180 درجة.

شبه منحرف مختلف الأضلاع

شبه المنحرف مختلف الأضلاع هو مضلع رباعي فيه:

• ضلعان اثنان متوازيان، وغير متساويان ويمثلان قاعدتيه.
• ضلعان غير متوازيين وغير متساويين، وله قطران غير متساويين ويتقاطعان في نقطة معينة.
• مجموع زوايا شبه المنحرف 360 درجة.

شبه منحرف قائم الزاوية

شبه المنحرف قائم الزاوية هو مضلع رباعي فيه:

• زاويتين قائمتين ارتفاع شبه المنحرف قائم الزاوية عبارة عن الضلع العمودي على القاعدة الكبرى.

شبه منحرف متساوي الساقين

شبه المنحرف متساوي الضلعين هو مضلع رباعي فيه:

• ضلعين متقابلين ومتوازيين.
• الضلعين الآخرين متقابلين ومتساويين في الطول، ولكن غير متوازيين.
• طول قطريه متساوي.
• زاويتي قاعدتيه متطابقتين.

شاهد أيضًا: كيف يحسب مساحة المعين

مساحة شبه المنحرف

مساحة شبه المنحرف، عبارة عن المنطقة الداخلية المحصورة والتي تقع ضمن حدود شبه المنحرف، وهناك عدة طرق لحساب مساحة شبه المنحرف، وهي كما يلي:

• يمكن إيجاد مساحة شبه المنحرف، من خلال رسم شبه منحرف مطابق تماما لشبه المنحرف الموجود.
• ثم قلبه والقيام بلصقه بجانب الشكل الأول، إذ سينتج من التصاق الشكل الأول مع الشكل الثاني متوازي أضلاع.
  • حيث يكون فيه مساحة شبه المنحرف الأول= مساحة شبه المنحرف الثاني، وحيث أن شبه المنحرف يمثل نصف متوازي الأضلاع.
  • فإن: مساحة شبه المنحرف= نصف مساحة متوازي الأضلاع الناتج في الرسم، وطول قاعدة متوازي الأضلاع تمثل طول قاعدته المتكونة من قاعدتي شبه المنحرف (الأول+ الثاني)، بينما ارتفاع متوازي الأضلاع هو نفسه ارتفاع شبه المنحرف.

• إذًا مساحة شبه المنحرف= 0.5 (طول قاعدة متوازي الأضلاع ×الارتفاع).
• أي مساحة شبه المنحرف= 0.5 (مجموع القاعدتين ×الارتفاع).

ويمكن استخدام القانون الآتي:

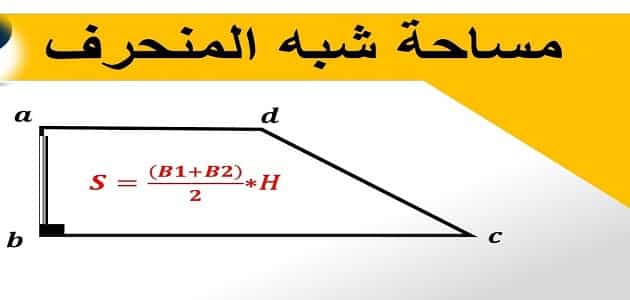
• مساحة شبه المنحرف= الارتفاع × (القاعدة الأولى+ القاعدة الثانية) ÷2).
• أما إذا كانت المعطيات طول القطعة المتوسطة الواصلة بين جانبين شبه المنحرف فبالتالي إن: مساحة شبه المنحرف= الارتفاع ×طول القطعة المتوسطة.
• إذا كانت المعطيات هي مساحة شبه المنحرف، فبالتالي يمكن إيجاد الارتفاع وطول القاعدة،
• ارتفاع شبه المنحرف=2×المساحة ÷ مجموع القاعدتين.
• طول القاعدة=(2×المساحة÷الارتفاع) -طول القاعدة الأخرى.

أمثلة على حساب مساحة شبه المنحرف

بعض الأمثلة التوضيحية التي تبين كيفية حساب مساحة شبه المنحرف وهي كما يلي:

مثال1

• شبه منحرف، فيه طول القاعدة الأولى=2 سم، وطول القاعدة الثانية= 4 سم، أما ارتفاعه = 3 سم، أوجد مساحته.

الحل

• قانون مساحة شبه المنحرف= 0.5× (مجموع طولي القاعدتين) × الارتفاع.
• يتم تعويض طول القاعدة الأولى والثانية والارتفاع في القانون.
• مساحة شبه المنحرف=3×(2+4) × 0.5
• ومساحة شبه المنحرف= 3×(6) × 0.5
• مساحة شبه المنحرف= 3×3
• إذًا: مساحة شبه المنحرف= 9 سم².

مثال2

• أرض على شكل شبه منحرف مساحتها تساوي
• 300 م²، إذا علمت أن مجموع طولي قاعدتيه يساوي 30 م، احسب ارتفاعها.

الحل

• قانون مساحة شبه المنحرف= 0.5× (مجموع طولي القاعدتين) × الارتفاع.
• يتم تعويض قيمة المساحة =300 م²،
• مجموع طولي الضلعين=30 م في القانون كالآتي: 300= 0.5×(30) × الارتفاع.
• 300= 15× الارتفاع،
• بقسمة الطرفين على العدد 15،
• تصبح المعادلة: 20 م= الارتفاع،
• الارتفاع = 20 م.

مثال3

• شبه منحرف فيه مجموع طولي القاعدتين يساوي 40 دسم، أما ارتفاعه فيساوي 18 دسم، احسب مساحة شبه المنحرف.

الحل

• قانون مساحة شبه المنحرف= 0.5× (مجموع طولي القاعدتين) × الارتفاع.
• يتم تعويض مجموع طولي القاعدتين والارتفاع في القانون.
• مساحة شبه المنحرف=18×(40) × 0.5
• مساحة شبه المنحرف= 18×20
• إذًا: مساحة شبه المنحرف=360 دسم².

مثال4

• شبه منحرف فيه طول القطعة المتوسطة يساوي 14 أما ارتفاعه يساوي 10 سم، احسب مساحته. الحل

• إذا علم طول القطعة المتوسطة الواصلة بين جانبين شبه المنحرف فإن:
• مساحة شبه المنحرف= الارتفاع ×طول القطعة المتوسطة.
• مساحة شبه المنحرف=10× 14 مساحة شبه المنحرف= 140سم²

محيط شبه المنحرف

• محيط أي شكل هندسي هو عبارة عن مجموع قياس حواف هذا الشكل، فبالتالي أن محيط شبه المنحرف يساوي طول الحافة الأولى+ طول الحافة الثانية+ طول الحافة الثالثة+ طول الحافة الرابعة.
• إذًا: فإن محيط شبه المنحرف يساوي مجموع أطوال حوافه.

أمثلة على حساب محيط شبه المنحرف

بعض الأمثلة التي توضح كيفية حساب محيط شبه المنحرف، وهي كما يلي:

مثال1

• سجادة على شكل شبه منحرف، فيها أطوال حوافها الأربعة على التوالي،5 م، 15م، 12 م،6 م، أوجد مساحته

الحل

• قانون محيط شبه المنحرف= مجموع أطوال الحواف.
• هكذا يتم تعويض أطوال الأضلاع في القانون.
• محيط السجادة= 5+ 15+ 12+ 6.
• هكذا إذًا: محيط السجادة= 38 م.

مثال2

• هكذا ورقة على شكل شبه منحرف، إذا علمت أن طول حوافها الأربعة على التوالي،2 سم، 1 سم، 3 سم، 1، 2.5 أوجد محيط الورقة.

الحل

• قانون محيط شبه المنحرف=مجموع أطوال الحواف. يتم تعويض أطوال الأضلاع في القانون.
• محيط الورقة= 2+1+3+2.5
• هكذا إذًا: محيط الورقة= 8.5 سم.

مثال3

لوح من الخشب على شكل شبه منحرف، إذا علمت أن طول الحواف الأربعة على التوالي،

• 14 سم، 10 سم، 13 سم،8 سم، أوجد محيط اللوح الخشبي

الحل

• قانون محيط شبه المنحرف=مجموع أطوال الحواف. يتم تعويض أطوال الأضلاع في القانون.
• محيط اللوح الخشبي= 14+10+13+8.
• هكذا إذًا: محيط اللوح الخشبي= 45 سم.

شاهد أيضًا: كيف يحسب مساحة المعين

هكذا ومن هنا نكون ختمنا معكم اليوم مقالنا عن مساحة شبه المنحرف ونرجو أن تكون المعلومات التي قدمناها في موقعكم المفضل ملزمتي قد أفادتكم، لا تنسوا لايك وشير للمقال.