ماذا تعرف عن المضلعات وأنواعها

ماذا تعرف عن المضلعات وأنواعها تتنوع وتتعدد الأشكال الهندسية باختلاف أبعادها، وإشكالها، فهناك أشكالًا ثنائية الإبعاد، وأشكالًا أخرى ثلاثية الأبعاد وغيرها، كما أن هناك أشكالاً هندسية منتظمة الشكل، وأشكالًا أخرى غير منتظمة الشكل.

حيث إن الأشكال الهندسية تحتل مساحة كبيرة من حياة الإنسان ومنها المربع والمستطيل، والمعين، والدائرة وغيرها من الأشكال الهندسية.

ماذا تعرف عن المضلعات وأنواعها

• علم المضلعات هو فرع من فروع الهندسة الرياضية، إذ إن المضلع عبارة عن خط مستقيم مغلق يلتقي مع عدة مضلعات مستقيمة ليتكون في النهاية شكل هندسي.
• فعلى سبيل المثال الدائرة لا تعتبر مضلعًا وذلك لعدم وجود أضلاع أو زوايا في الدائرة، وأيضًا أي شكل مفتوح لا يعتبر مضلعًا.
• وذلك لأن من أهم شروط اعتبار الشكل مضلعًا، هو أن يكون هذا الشكل مغلقًا، وأن يتكون من عدد من الزوايا وهي عبارة عن الزوايا التي تقع بين ضلعين.

شاهد أيضًا: كيف يحسب مساحة المعين

المضلع

المضلع (Polygon)، هو أي شكل هندسي ثنائي الأبعاد، يتكون من خطوط مستقيمة، وقد اشتقت كلمة مضلع (Polygon) من كلمة يونانية.

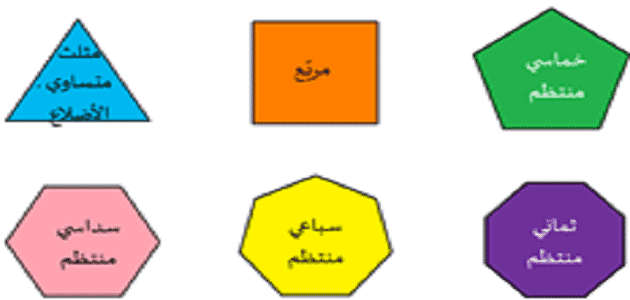
معناها العديد من الزوايا، ومن الأمثلة على المضلع المثلث أو الثلاثي، والرباعي، والخماسي، والسداسي، ويتم التعرف على عدد جوانب المضلع عن طريق اسمه:

• الشكل الذي يتم رسمه من خلال توصيل ثلاثة خطوط مستقيمة يسمى مثلثًا.
• والشكل الذي يتم رسمه من خلال توصيل أربعة خطوط مستقيمة يسمى رباعيًا.
• الشكل الذي يتم رسمه من خلال توصيل خمسة خطوط مستقيمة يسمى خماسيًا.
• إذا كان الشكل يحتوي على خطوط منحنية، أو لا ترتبط فيه الخطوط بشكل كامل، فلا يمكن أن يطلق عليه المضلع.

أجزاء وخصائص المضلع

المضلع يتكون من عدة أجزاء وهي:

• الزاوية (angle) وهي الزاوية المحصورة التي تتكون نتيجة تقاطع جانبين من المضلع.
• الجانب (Side) وهو الضلع أو الخط من الخطوط المستقيمة التي تشكل المضلع.
• القمة أو الرأس (Vertex) هي نقطة التقاء أي ضلعين (جانبين) من الجوانب لتشكيل زاوية.
• القطر (Diagonal) وهو الخط الواصل بين أي رأسين غير متجاورين. المحيط (Perimeter).
• وهو مجموع طول جميع (أضلاع) جوانب المضلع. المساحة (Area) وهي المساحة المحصورة داخل المضلع.

تصنيف المضلعات

• المضلع هو عبارة عن خط منكسر، مغلق يتكون من اتحاد عدد من القطع المستقيمة، وهو شكل هندسي له زوايا، وأضلاع، ورؤوس.
• يتكون المضلع من عدد رؤوس = عدد أضلاعه = عدد الرؤوس.
• ومن أهم الخصائص التي يجب أن تتوافر في الشكل الهندسي لاعتباره مضلعًا، هو أن لا يقل عدد أضلاع الشكل الهندسي عن ثلاثة أضلاع، وأن يكون مجموع الزوايا مجتمعة لا يقل عن 180 درجة.

وتصنف المضلعات حسب عدد الخطوط المكونة الشكل وهي كالتالي:

• المضلع الثلاثي (المثلث)، هو مضلع له ثلاثة أضلاع، وثلاثة رؤوس، وثلاثة زوايا متساوية مقدار كل منها 60 درجة، بحيث يكون مجموعها 180 درجة.
• المضلع الرباعي، هو مضلع له أربع أضلاع، وأربع رؤوس، وأربع زوايا مقدار كل منها 90 درجة.
• والمضلع الخماسي، هو مضلع له خمسة أضلاع، وخمسة رؤوس، وخمسة زوايا متساوية مقدار كل منها 108 درجة.
• المضلع السداسي (المسدس)، هو مضلع له ستة أضلاع، وستة رؤوس، وستة زوايا متساوية مقدار كل منها 120 درجة.
• والمضلع الثماني، هو مضلع له ثمانية أضلاع، وثمانية رؤوس، وثمانية زوايا متساوية مقدار كل منها 135 درجة.

المضلعات وأنواعها

توجد ثلاثة أنواع من المضلعات، وهي كما يلي:

• مضلع متساوي الأضلاع، وهو عبارة عن مضلع كل جوانبه (أضلاعه)متساوية في الطول.
• مضلع متساوي الزوايا، وهو عبارة عن مضلع جميع زواياه متساوية.
• ومضلع منتظم، وهو عبارة عن مضلع متساوي الأضلاع والزوايا.
• المضلعات المنتظمة، المضلعات المنتظمة أو المضلعات المتشابهة هي تلك المضلعات التي يكون لها نفس الشكل، ولكن بقياسات مختلفة، إذ أنه لا يشترط في المضلعات المتشابهة أن تمتلك نفس مقدار القياس.
• جميع زوايا المضلعات المتشابهة تكون متناظرة ومتطابقة.
• جميع أطوال أضلاع المضلعات المتشابهة تكون متناظرة.

شاهد أيضًا: أنواع المثلثات حسب الزوايا

المضلعات غير المنتظمة

• أسماء المضلعات تحدد حسب أبرز خاصية به، وهنا المضلع غير المنتظم أي الذي لا تتساوى فيه أطوال أضلاعه، وكل زاوية من زواياه تأخذ قيمة مختلفة تمامًا عن الأخرى.

المضلع المحدب

يطلق على المضلع اسم المحدب، عندما يكون مضلعًا بسيطًا، ومجموع الزوايا الداخلية لهذا المضلع أقل من 180 درجة، وعند امتداد أضلاعه فإنها لا تتقاطع ومن أهم الخصائص التي يجب أن تتوافر في الشكل حتى يعتبر مضلعًا محدبًا ما يلي:

• أن يكون قياس كل زاوية داخلية يساوي أو أقل من 180 درجة.
• وأن يكون مجموع قياس الزوايا الخارجية للشكل يساوي 360 درجة.
• أن تقع القطع المستقيمة للمضلع بين رأسين سواء متجاورين أو غير متجاورين، ولكن شرط أن تمر داخل المضلع أو تقع على محيطه.
• أي مثلث متدهور يعتبر مضلعًا محدبًا.

أمثلة على المضلعات وأنواعها

هناك عدد من الأشكال الهندسية التي تمثل مضلعًا، ومن أكثر أنواع المضلعات شيوعًا، واستخدامًا ما يلي:

• متوازي الأضلاع (Parallelogram)، وهو مضلع رباعي الشكل أي (له أربعة جوانب)، كل جانبين متوازيان ومتساويان.

له عدة خصائص تميزه منها ما يلي:

• متوازي الأضلاع شكل ثنائي الأبعاد.
• كل ضلعين متقابلين متوازيين.
• كل ضلعين متقابلين متساويين في الطول.
• مجموع كل زاويتين متتاليتين 180 درجة.
• كل زاويتين متقابلتين متساويتين في القياس.
• مساحة متوازي الأضلاع = طول القاعدة × الارتفاع.
• محيط متوازي الأضلاع = مجموع أطوال أضلاعه.

المربع (Square)

وهو عبارة عن حالة من المستطيل جميع جوانبه متساوية، له عدد من الخصائص منها ما يلي:

1. كل ضلعين متقابلين متوازيين.
2. جميع زوايا المربع متساوية في القياس.
3. المربع حالة خاصة من المعين، لأن إحدى زواياه قائمة.
4. قطرا المربع متعامدان ومتساويان في الطول وينصف كل منهما الآخر.
5. محيط المربع = 4 × طول الضلع.
6. مساحة المربع = طول الضلع × نفسه.

المعين (Rhombus)

وهو عبارة عن حالة من متوازي الأضلاع جوانبه الأربعة متساوية، وله عدد من الخصائص منها ما يلي:

• جميع أضلاع المعين متساوية في الطول.
• كل ضلعين متقابلين متوازيين.
• كل زاويتين متقابلتين متساويتين في القياس.
• مجموع كل زاويتين متتاليتين 180 درجة.
• قطرا المعين متعامدان وينصف كل منهما الآخر.
• محيط المعين = 4× طول الضلع.
• مساحة المعين = طول القاعدة × الارتفاع.

المستطيل (Rectangle)

وهو عبارة عن حالة من متوازي أضلاع تكون جميع الزوايا فيه قائمة، له عدد من الخصائص وهي كما يلي:

1. كل ضلعين متقابلين متوازيين ومتساويين في الطول.
2. المستطيل له قطران متساويان في الطول وينصف كل منهما الآخر.
3. مساحة المستطيل = الطول × العرض.
4. محيط المستطيل = 2× (الطول + العرض).

محيط ومساحة المضلع

• ومحيط المضلع يمكن أن يتم حساب محيط المضلع عن طريق جمع أطوال جميع أضلاعه.
  • وتستخدم الوحدات الخطية لقياس المحيط، مثل: المتر، أو البوصة، أو الميل، أو القدم.
• مساحة المضلع يمكن أن يتم حساب مساحة المضلع بحساب عدد الوحدات المربعة التي توجد في الشكل، وتستخدم الوحدات المربعة لقياس مساحة المضلع مثل: المتر المربع، أو قدم مربع، وغيرها.

مثال(1)

• هكذا أوجد محيط المضلع المنتظم خماسي الشكل طول ضلعه 6 سم.

الحل

• المحيط = مجموع أطوال أضلاع المضلع.
• المحيط =6+6+6+6+6.
• = 5 × 6.
• المحيط =30 سم.

مثال(2)

• هكذا أوجد محيط المضلع السداسي المنتظم الذي طول ضلعه 4 سم.

الحل

• المحيط = 4 + 4 + 4 + 4 + 4 + 4.
• = 6 × 4 سم.
• عدد الأضلاع =6 طول الضلع = 4 سم.
• محيط المضلع السداسي المنتظم = 6 × طول الضلع.
• محيط المضلع السداسي المنتظم = 6×6=36 سم.

شاهد أيضًا: كيف نحسب المساحة والمحيط

هكذا ونكون بهذا أنجزنا مقالنا اليوم عن ماذا تعرف عن المضلعات وأنواعها ونرجو أن تكون المعلومات المقدمة مفيدة ليكم، لا تنسوا لايك وشير للمقال لتوصيل المعلومة إلى أكبر عدد للاستفادة.