بحث عن متوازي الأضلاع وخواصه

مقدمة بحث عن متوازي الأضلاع وخواصه :.

متوازي الأضلاع هو شكل هندسي له أربعة أضلاع بحيث يكون كل ضلعين يقابلون بعضهم البعض متوازيان لبعضهمها، وهذا التوازي يجعل كل ضلعين متوازيين متساويين في الطول، بالإضافة إلى تساوي الزوايا الخاصة بهم.

وأي قُطر يقطع متوازي الأضلاع يجعله يقوم بتقسيمه إلى شكلين متساويين، وتبلغ مساحة زوايا متوازي الأضلاع الأربعة ثلاثمائة وستون درجة، ومتوازي الأضلاع يشبه إلى حد كبير شكل المُعيَن.

الخصائص العامة لمتوازي الأضلاع :.

لمتوازي الأضلاع عدد من الخصائص التي ينفرد بها دون الأشكال الهندسية الأخرى، وهى كما يلي :

• عندما يتم تقسيم متوازي الأضلاع نحصل على شكلين مختلفين هندسيين لكنهم متطابقين تماماً في الأطوال وفي الأربع زوايا منه.
• يتميز متوازي الأضلاع بأن كل زاوية تقابل الأخرى تساويها في المساحة.
• كل ضلعين متقابلين في متوازي الأضلاع متساويين تماماً في المقدار.
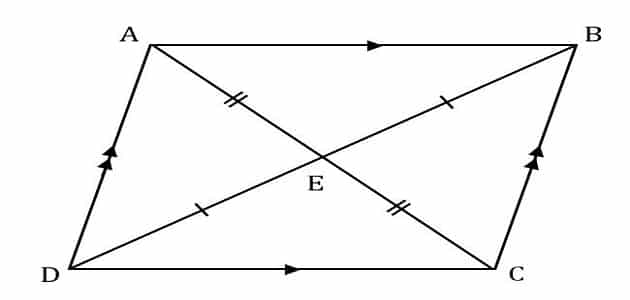
• عندما يتم رسم قطرين في متوازي الأضلاع تكون نقطة المركز في شكل تناظري لشكل متوازي الأضلاع ككل، والنقطة المركزية تسمى مركز متوازي الأضلاع.
• تبلغ مساحة متوازي الأضلاع الضعف من مساحة المثلث الذي يتكون من ضلعين وقُطر واحد.
• متوازي الأضلاع من أهم ميزاته أن كل قُطر يتم رسمه فيه يكون مقداره نصف القُطر الأخر.

شاهد ايضًا : بحث كامل عن جمال السجينى وأعماله

محيط ومساحة متوازي الأضلاع :.

إذا إفترضنا أن هناك متوازي أضلاع مساحته تبلغ القيمة ” أ “ والمعادلة التي تمكنّا من حساب مساحة متوازي الأضلاع تكون بمعرفة طول إرتفاع متوازي الأضلاع وقاعدته.

إذن القانون هو ” أ = الإرتفاع × طول القاعدة “ وطول القاعدة يتم حسابه من قياس أي ضلع موجود من أضلاع متوازي الأضلاع.

أما بالنسبة للمساحة فيمكن حسابها عن طريق معرفة طول أي ضلعين بجانب بعضهما، وقيمة الزاوية الواقعة بينهما، والطريقة الأخرى لحساب المساحة هى المعرفة بأطوال أي قُطرين ونسبة قياس أي زاوية من الزوايا المحصورة بين هذين القطرين.

أما محيط متوازي الأضلاع فيمكن حسابه بكل سهولة بمعرفة قياس أطوال أي ضلعين بجانب بعضهما البعض في المتوازي.

حالات خاصة بمتوازي الأضلاع :.

هناك بعض الحالات التي يتحول فيها شكل متوازي الأضلاع إلى شكل أخر، وهى كما يلي :

• إذا كانت الأقطار متعامدة أو متساوية في الطول، وخاصةً بين ضلعين بجانب بعضهم البعض، يتحول متوازي الأضلاع في هذه الحالة إلى شكل مُعَين.
• وإذا كانت أقطار متوازي الأضلاع متساوية أو كانت أحد الزوايا فيه قائمة أي تساوي تسعين درجة، يتحول الشكل إلى مستطيل.
• إذا تحول متوازي الأضلاع إلى معين ومستطيل يمكن أن يتحول الشكل الذي بعد ذلك إلى مربع.

شروط يجب توافرها ليكون الشكل الهندسي متوازي أضلاع :.

• إذا تطابق أي ضلعان متقابلان في أي شكل هندسي أصبح شكلاً لمتوازي أضلاع.
• وإذا تطابق وتقابل وتوازى أي ضلعين في أي شكل رباعي تحول إلى متوازي أضلاع.
• إذا كانت الأقطار الموجودة في الشكل تقوم بتنصيف بعضها البعض تحول الشكل إلى متوازي أضلاع.
• وإذا تساوت الزوايا التي تقابل بعضها تحول الشكل إلى متوازي أضلاع.
• إذا كانت نتيجة قياس أي زاويتان متقابلتان مائة وثمانون درجة أصبح الشكل متوازي أضلاع.

ومتوازي الأضلاع هو أحد الأشكال الثنائية الأبعاد ويتم رسمه في مستويات ديكارتيه على محاور سينيه وصادية.

كل الأشكال الثنائية لها مساحة خاصة بها، وقد تم عمل مساحة متوازي الأضلاع من خلال المساحات للمثلث والمستطيل، لأن متوازي الأضلاع إذا تمت تجزئته سوف نحصل على مستطيل ومثلث.

وقانون مساحة متوازي المستطيلات = طول القاعدة × طول الإرتفاع الساقط على القاعدة، أما محيط متوازي الأضلاع فمعادلته هى : مجموع أطوال أضلاعه كاملة.

شاهد ايضًا : بحث عن حالات المادة وتحولاتها

كيف يتم رسم متوازي الأضلاع :.

حتى يُمكن رسم متوازي الأضلاع لابد من معرفة طول ضلعين متجاورين، وكذلك القياس الخاص بالزاويا التي تقع بينهم، وطريقة رسمه هى كما يلي :

• نقوم برسم خط مستقيم قياسه أربعة سنتيمتر.
• نضع المنقلة بحيث تكون نقطة المنتصف فيها على طرف أحد القطع المرسومة، وأن يكون قياس هذه الزاويا ثمانون درجة.
• نقوم بإيصال الطرف الخاص بالقطعة المستقيمة والمكان الذي تم وضع المنقلة فيه، وهذا سوف ينتج عنه ضلع قياسه أربعة سنتيمتر.
• نضع البرجل في الطرف الحُر من القطعة المستقيمة التي طولها أربعة سنتيمتر، ثم نفتح البرجل بقياس ثلاثة سنتيمتر ونرسم قوس.
• نضع البرجل عند طرف القطعة المستقيمة الأخرى الحره التي قياسها ثلاثة سنتيمتر، ثم نقوم بفتح البرجل بطول يصل إلى أربعة سنتيمتر، ونرسم قوس بحيث يتقاطع مع ما رسمناه من قوس في نقطةٍ ما.
• نقوم بعد ذلك بإيصال النقطة التي تقاطع فيها القوسين مع الطرفين، وهذا من خلال إستخدام مسطرة، هنا نغلق الشكل تماماً وسوف نحصل على شكل لمتوازي الأضلاع.

بعض الأشكال الرباعية الأخرى :.

• المُعين :.

  • يختلف عن متوازي الأضلاع بأن كل أضلاعه متساوية.
  • وأقطاره متعامدة ويقوم كل قُطر بتنصيف الأخر ويقومون بتنصيف زاوية الرأس.
  • وكل زاويتان متتاليتان فيه قياسهم مائة وثمانون درجة، لكن أطواله الأربعة تتساوى في القياس.

• المربع :.

• هو أحد أنواع متوازي الأضلاع لكن يختلف عنه بأن كل الزوايا الموجودة في المربع قائمة أي تساوي تسعون درجة.
• والأضلاع متطابقة والأقطار متعامدة ومتطابقة ومتناصفة، أما محيط المربع فيمثل أربع أضعاف طول ضلع واحد منه.

• مستطيل :.

• هو أيضاً واحد من أنواع متوازي الأضلاع.
• لكن يختلف عنه بأن كل زواياه أيضاً قائمة والأقطار متناصفة ومتطابقة.
• لكن محيطه يكون ضعف المجموع الكُلي للعرض والطول.

• شبه المنحرف :.

  • له شكلان هم ” شبه منحرف متساوي الساقين – شبه منحرف به ضلعين متوازيين “.

• الدالتون :.

• أحد أنواع متوازي الأضلاع لكنه يتكون من مثلثين متساويين في الساق.
• ويشتركون معاً في قاعدة واحدة، لكنه يتميز بأن أقطاره متعامدة على بعضها، وكل زاوية جانبية متساوية للأخرى.

خاتمة بحث عن متوازي الأضلاع وخواصه :.

• قدمنا لكم بحث مفصل عن متوازي الأضلاع أحد الأشكال الهندسية الهامة في علم الرياضيات وخاصةً في الهندسة.
  • وقومنا بعرض خصائصه التي يتميز بها وحساب مساحته ومحيطه وأضلاعه.
  • وقدمنا حالات خاصة فيها يتحول متوازي الأضلاع إلى أشكال أخرى كالمعين أو المربع أو المستطيل.
• كما قدمنا أيضاً عدة أنواع من متوازي الأضلاع وخاص كل نوع منها.
  • وما هى أهم الأشياء التي يتميز بها، كما قدمنا لكم أيضاً أبسط الطرق لكيفية رسم متوازي الأضلاع باستخدام الأدوات الهندسية البسيطة مثل المسطرة والبرجل والمنقلة.
• والجدير بالذكر أن متوازي الأضلاع هو أحد الأشكال الهندسية التي يتم طلب رسمها في الإمتحانات في المراحل الدراسية المختلفة.
  • وهذا ما دفعنا لتقديم هذا البحث وكتابته إليكم بأبسط الطرق المُمكنة حتى تتمكنوا من أن تحصلون على أعلى الدرجات وتحصيل أفضل العلم والنتائج وتحقيق النجاح.

وصلنا إلى نهاية بحث اليوم عن متوازي الأضلاع وخواصه نتمنى أن تتابعونا دائماً لكي يصلكم كل جديد وكل ما هو مفيد من الأبحاث العلمية الهامة والمعلومات العامة التي تحرص أسرة الموقع على تقديمها لكل متابعيها.