مساحة المثلث ومحيطه وحجمه

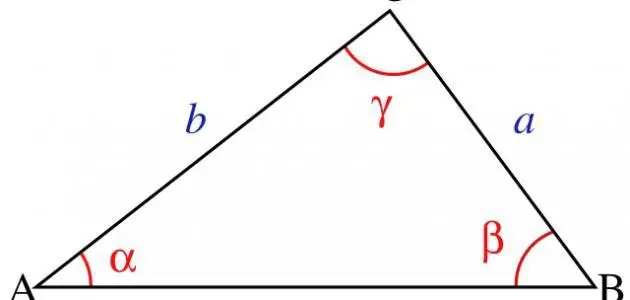
مساحة المثلث ومحيطه وحجمه:

الأنواع المختلفة للمثلثات :.

 الأول تبعاً لأطوال أضلاعه :

وهو يعتمد على مساحة طول كل ضلع من أضلاع المثلث.

فإن تساوت هذه الأضلاع في الطول في هذه الحالة يتم إطلاق اسم ” مثلث متساوي الأضلاع.

وأهم ما يميز هذا النوع من المثلثات هو أن كل زاوية من زواياه تبلغ مساحتها ستين درجة.

وإذا كان هناك تساوي بين مساحة ضلعين فقط، فيطلق على اسم المثلث في هذه الحالة ” مثلث متساوي الساقين.

ويتميز هذا النوع من المثلثات بأن الزاويتين المتقابلتين متساويتين.

أما النوع الأخير من المثلثات فهو مثلث يختلف أطوال أضلاعه عن بعضها البعض وكذلك زواياه.

شاهد ايضًا : معلومات عن مدرسة البكالوريا الحكومية الدولية

أما النوع الثاني :

فقد قام العلماء بتنصيف أنواع المثلثات فيه على أساس قياس الزوايا المختلفة الداخلية به.

فإن كان المثلث يحتوي على زاوية قائمة قياسمها تسعين درجة سمي ” مثلث قائم الزاوية “.

أما إن كان هناك زاوية في المثلث تبلغ نسبتها أكثر من تسعين درجة فيسمى ” مثلث منفرج الزاوية.

أما النوع الأخير من المثلثات إن كانت جميع زواياه في القياس أصغير من تسعين درجة فيسمى ” بمثلث حاد الزوايا “.

حساب محيط وحجم المثلث :.

المحيط الخاص بالمثلث له قاعدة معروفة، وهى كالتالي :

محيط المثلث = مجموع أطوال أضلاعه الثلاثة.

وسوف نأخذ بعض الأمثلة على ما سبق ذكره وهى كالتالي :

المثال الأول :

إوجد حساب محيط المثلث المختلف الأضلاع الذي ضلعه الأول يساوي تسعة عشر سنتيمتر.

والضلع الثاني منه يساوي خمسة عشر خمسة عشر سنتيمتر والضلع الثالث يساوي تسعة سنتيمتر.

الإجابة : نقوم بعملية جمع بسيطة لجميع الأطوال الخاصة بالمثلث، فنطبق القاعدة السابق ذكرها.

والتي تقول أن المحيط الخاص بالمثلث بيساوي مجموع أطوال أضلاعه الثلاثة.

إذًا : محيط المثلث بيساوي ثلاثة وأربعون سنتيمتر.

المثال الثاني :

أوجد محيط المثلث الذي أضلاعه تكون أربعة سنتيمتر، ثلاثة سنتيمتر، خمسة سنتيمتر.

الإجابة : بالقيام بالتعويض بكل المعطيات من خلال القانون الخاص بمحيط المثلث.

فإن إجابة هذه المسألة تكون كالتالي :

محيط المثلث بيساوي مجموع أضلاعه.

إذًا : فمحيط المثلث هو  إثنا عشر سنتيمتر.

المثال الثالث :

إوجد محيط المثلث الذي يكون طول ضلعه الأول بيساوي خمسة سنتيمتر.

أما الضلغ الثاني فهو يساوي سبعة سنتيمتر والضلغ الأخير يساوي تسعة سنتيمتر.

الإجابة : كما عرضنا مسبقاً فإن محيط المثلث بيساوي مجموع أضلاعه الثلاث.

إذًا : محيط المثلث يساوي واحد وعشرون سنتيمتر.

المثال الرابع :

إوجد محيط المثلث المتساوي الأضلاع الذي يبلغ طول الضلع منه خمسة سنتيمتر.

الإجابة : بما إننا نعلم أن من خواص المثلث المتساوي الأَضلاع أن كل أطوال أضلاعه متساوية.

فتكون الإجابة هى خمسة + خمسة + خمسة = خمسة عشر سنتيمتر.

المثال الخامس :

إذا كان هناك مثلث مستاوي الساقين، ويبلغ محيطه سبعة سنتيمتر.

ويبلغ كل ضلع من أضلاعه المتساوية ثلاثة سنتيمتر، فما هو طول الضلع رقم ثلاثة.

الإجابة : بتطبيق قانون محيط المثلث والمعادلة الخاصة به، نجد أن محيط المثلث بيساوي مجموع كلاً من :

الضلع الأول + الضلع الثاني + الضلع الثالث

سبعة = ثلاثة + ثلاثة + الطول الخاص بالضلع الثالث

سبعة = ستة + الطول الخاص بالضلع الثالث

إذًا : عندما نقوم بطرح العدد رقم ستة من المحيط سيعطي لنا الطول الخالص بالضلع الثالث، وهو يساوي واحد.

وبهذا المثال رقم خمسة نكون قد تعرفنا كيف نأتي بطول الضلع الثالث بمنتهى السهولة واليسر.

حساب مساحة المثلث :.

تم تعريف المساحة الخاصة بأي مثلث بأنها العملية القياسية التي تحسب مساحة سطح محصورة بين أضلاع المثلث الثلاثة.

هكذا وقد تعددت الطرق التي ممكن بها عمل تلك العملية الحسابية ومنها ما يلي :

هناك بعض الحقائق التي وضعها علماء الرياضيات تتعلق بالمثلث وهى كما يلي :

وهكذا نكون قد عرضنا لكم أعزائنا متابعين موقع ملزمتي التعليمي الشامل بشكل دقيق ومفصل مساحة المثلث ومحيطه وحجمه.

كما عرضنا بعض الحقائق الهامة جداً عن المثلثات وفقاً لما قاله علماء الرياضيات، كما ذكرنا أيضاً في موضوعنا اليوم الأنواع المختلفة للمثلثات.

شاهد ايضًا : معلومات عن طائر النسر مع الصور

هكذا وتستطيعوا أن تجدوا الكثير من المعلومات العامة المفيدة في قسم معلومات عامة الذي يحرص دائماً على تقديم كل ما هو مفيد وهام.

حتى يقوم بإثراء الثقافة داخل نفوس الطلبة، ونتمنى أن تكونوا قد إستفدتم مما قدمناه لكم اليوم، ومع خالص تمنياتنا بالتوفيق لكم دائماً إن شاء الله.