قانون حجم ومساحة المكعب
قانون حجم ومساحة المكعب الأشكال الهندسية عالم كبير، يحتل مساحة واسعة من حياة الإنسان اليومية، وتتنوع هذه الأشكال الهندسية وتختلف سواء كان الاختلاف في الشكل أو في الأبعاد.
ومن هذه الأشكال الهندسية، المكعب الذي يتواجد في أشكال كثيرة في حياة الفرد (حجر النرد، ومكعبات الثلج، ومكعبات السكر وغيرها).
تعريف المكعب
المكعب (Cube)، هو أحد أهم المجسمات الهندسية الثلاثية الأبعاد (الطول، والعرض، والارتفاع)، ويتكون المكعب مما يلي:
- عدد 6 أوجه يمكن رؤيتها بوضوح، حيث تقع هذه الأوجه في الأمام والخلف، وفي اليمين واليسار، وفي الأعلى والأسفل.
- أوجه المكعب على شكل مضلعات رباعية منتظمة الشكل.
- أوجه المكعب جميعها يمكن أن تكون قاعدًة له، وذلك لأنها متساوية في المساحة وجميع أضلاعها عمودية على بعضها البعض.
- أصل تسمية المكعب بهذا الاسم، يعود الى علم الحساب والجبر، إذ أن مصطلح مكعب العدد، يعني عدد مرات ضربه في نفسه ثلاث مرات، وبالصيغة الأسية يتم رفع العدد للقوة الثالثة (أس ثلاثة).
- على سبيل المثال، مكعب العدد 2، يكتب 2 على صورة 2³ = 2 ×2× 2، إذ أن حاصل ضرب العدد 2 في نفسه ثلاث مرات يساوي 8.
- من أمثلة المجسمات التي تمثل المكعب، (حجر النرد، ومكعبات الثلج، وخزان الماء) وغيرها الكثير.
أقرأ أيضًا: ما هو قانون شبه المكعب
خصائص المكعب
يتميز المكعب بعدد من الخصائص التي تميزه عن غيره من المجسمات الهندسية، ومن هذه الخصائص ما يلي:
- المكعب من المجسمات ثلاثية الأبعاد، إذ أن له طول، وعرض، وارتفاع.
أوجه المكعب مربعة فبالتالي:
- الطول= العرض= الارتفاع.
- يحتوي المكعب على ستة أوجه، وكل وجه من هذه الأوجه على شكل مربعًا، حيث تتساوى جميع الأوجه في الحجم والمساحة.
- يحتوي كل وجه من أوجه المكعب على 4 أضلاع، وبذلك يكون عدد أضلاع المكعب 12 ضلعًا، ويفصل كل ضلع بين وجهين متجاورين.
- ويحتوي المكعب على 8 زوايا و8 رؤوس، إذ تعتبر الرأس نقطة تلاقي ثلاث حواف معًا.
- الحجم (Volume)، هو الحيز أو المكان الذي تشغله المجسمات (ثلاثية الأبعاد)، أي أنه عدد الوحدات المكعبة التي تملأ المكان أو الحيز الذي يشغله هذا المجسم.
حجم المكعب
- معرفة حجم الأشكال والمجسمات أمرًا هامًا، فكثيرًا ما نحتاج إلى معرفة سعة خزان المياه، أو حجم قالب الجبنة.
- وغيرها من أمور الحياة اليومية، ويقاس حجم المكعب بالوحدات المكعبة، ويتم تحديد نوع الوحدة التي تستخدم في قياس حجم المكعب بناءًا على حجم المجسم.
- فإذا كان المجسم صغير الحجم يتم استخدام وحدة قياس صغيرة تناسبه، وإذا كان المجسم كبير الحجم يتم استخدام وحدة قياس كبيرة مناسبة له.
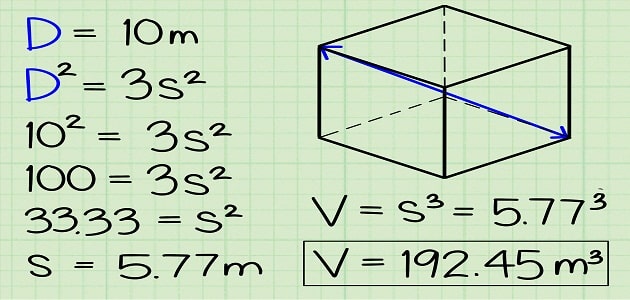
قانون حجم ومساحة المكعب
هناك عدد من الوحدات الشائعة التي تستخدم في قياس الأطوال مثل:( مم، أو سم، أو دسم، أو م)، وعندما يكون المطلوب هو الحجم تصبح هذه الوحدات:
- ( مم³، أو سم³، أو دسم³، أو م³)، وبناءًا عليه فإن: قانون حجم المكعب= (طول الضلع) ³.
أمثلة حساب حجم المكعب
بعض الأمثلة التي تبين كيفية حساب حجم المكعب كما يلي:
مثال1
- احسب حجم صندوق مكعب، إذا علمت أن طول أحد أضلاعه يساوي 3 م.
الحل
- قانون حجم المكعب = (طول الضلع) ³.
- يتم تعويض طول الضلع بالقانون:
- حجم الصندوق= (3) ³
- إذًا حجم الصندوق= 27 م³.
مثال2
- خزان مكعب الشكل، طول أحد أضلاعه 4 م، يراد ملؤه بالماء، فإذا كان سعر المتر الواحد من المياه 1.5 كم تكلفة تعبئة الخزان بالكامل؟
الحل
- أولًا: قانون حجم المكعب = (طول الضلع) ³.
- حجم الخزان= (4) ³. حجم الخزان= 64 م³.
- ثانيًا: التكلفة= ثمن المتر الواحد× حجم الخزان. التكلفة= 1.5×64=96 جنيهًا.
- إذًا: تكلفة ملء الخزان بالكامل هي 96 جنيهًا.
مثال3
- علبة على شكل مكعب، حجمها يساوي 125ملم³، احسب طول ضلعها.
الحل
- قانون حجم المكعب = (طول الضلع) ³.
- 125ملم³= (طول الضلع)³،
- (يتم أخذ الجذر التكعيبي للطرفين للحصول على طول الضلع).
- الجذر التكعيبي للعدد 125= 5.
- طول الضلع= 5 ملم.
شاهد أيضًا: ما الفرق بين العدد والرقم في الرياضيات
ثانيًا: -المساحة
- المساحة (Area)، هي المنطقة التي تقع داخل حدود وحواف الشكل المطلوب حساب مساحته، وتكون وحدة المساحة مربعة، (سم²، م²، كم²، وغيرها).
مساحة المكعب
- مساحة المكعب هي مجموع مساحات أوجهه الكاملة، ومن السهل إيجاد مساحة الأوجه في المكعب لأنها متساوية ومنتظمة وبناءً عليه فإن
- ومساحة المربع= طول الضلع مضروب في نفسه، مساحة المربع= (طول الضلع) ².
- ومساحة المكعب= مجموع مساحات أوجهه.
- بما أن أوجه المكعب هي 6 أوجه.
- فإن مساحة المكعب= (طول الضلع) ²+ (طول الضلع) ²+ (طول الضلع) ²+ (طول الضلع) ²+ (طول الضلع) ²+ (طول الضلع) ².
- مساحة المكعب= عدد الأوجه× (طول الضلع) ²، مساحة المكعب الكلية = 6× (طول الضلع) ².
- أما المساحة الجانبية للمكعب، يمكن حسابها كما يلي: المساحة الجانبية للمكعب= 4× (مربع طول الضلع) أمثلة حساب مساحة المكعب
بعض الأمثلة التي تبين كيفية حساب مساحة المكعب كما يلي:
مثال1
- احسب المساحة اللازمة لطلاء خزان مياه، إذا علمت أن طول أحد أضلاعه يساوي 3 م.
الحل
- قانون مساحة المكعب = مجموع مساحات أوجهه.
- مساحة الخزان= 6×(3) ²، مساحة الخزان= 6×9. مساحة الخزان= 54 م².
مثال2
- احسب مساحة حجر نرد، إذا علمت أن طول أحد جوانبه يساوي 0.5 سم.
الحل
- قانون مساحة المكعب = مجموع مساحات أوجهه، مساحة الحجر= 6×(0.5) ².
- مساحة الحجر= 6×0.25.
- مساحة الحجر= 1.5سم².
مثال3
- احسب مساحة ورق التغليف اللازم في تغليف صندوق مكعب الشكل، إذا علمت أن طول حرفه 4 سم.
الحل
- قانون مساحة المكعب= عدد أوجه المُكعب× (طول الضلع) ².
- مساحة الصندوق= 6×(4) ².
- مساحة الصندوق= 6×16.
- إذًا: المساحة اللازمة لتغليف الصندوق هي 96 سم².
مثال4
- إذا تم معرفة مساحة خمسة أوجه في مكعب، ومساحة كل منها هي 25سم²، أوجد مساحة الوجه السادس في هذا المكعب.
الحل
- نتيجة لأن أطوال الأضلاع في المكعب متساوية، فإن الأوجه متساوية كذلك، وبهذا فإن مساحاتها متساوية: مساحة الوجه السادس= 25سم².
مثال5
- أوجد المساحة الكلية لمكعب طول ضلعه 5 سم، إن كان بدون غطاء.
الحل
- المساحة الكلية للمكعب= 6× (مربع طول الضلع) المساحة الكلية للمكعب (بالأوجه الستة) = 6×(5) ² المساحة الكلية للمكعب (بالأوجه الستة) = 150 سم² المساحة الكلية للمكعب بدون غطاء،
- أي أن عدد أوجه المكعب يساوي خمسة أوجه: المساحة الكلية للمكعب (بدون غطاء) = 5× (مربع طول الضلع) المساحة الكلية للمكعب (بدون غطاء) = 5×(5) ² المساحة الكلية للمكعب (بدون غطاء) = 125 سم²
الفرق بين المكعب ومتوازي المستطيلات
متوازي المستطيلات (Cuboid)، هو شكل هندسي ثلاثي الأبعاد، يطلق عليه أيضًا شبه المكعب.
- من الأخطاء الشائعة اعتبار متوازي المستطيلات والمكعب مجسمًا واحدًا.
- يختلف متوازي المستطيلات عن المكعب، بأن له ستة أوجه مستطيلة الشكل، في حين أن المكعب له ستة أوجه مربعة الشكل.
- كل مكعب هو متوازي مستطيلات، ولكن ليس كل متوازي مستطيلات مكعبًا.
- حساب حجم متوازي المستطيلات، هي نفس طريقة حساب حجم المكعب، ولكن بوجود اختلاف بسيط وهو أن أطوال أضلاع متوازي المستطيلات غير متساوية.
- حجم متوازي المستطيلات= طول القاعدة ×عرض القاعدة ×الارتفاع.
- حجم متوازي المستطيلات= مساحة القاعدة ×الارتفاع.
مثال
- إذا كان مجسمًا يبلغ طوله 3 سم، ويبلغ عرضه 8 سم، ويبلغ ارتفاعه 6 سم أوجد حجمه.
الحل
نتيجة لأن أطوال المجسم غير متساوية، فإن الشكل عبارة عن متوازي مستطيلات، ويحسب حجمه كما يلي:
- حجم متوازي المستطيلات= الطول × العرض × الارتفاع.
- وحجم متوازي المستطيلات= 3×8×6.
- حجم متوازي المستطيلات= 144 سم³.
موضوعات أخرى:
ومن خلال موقع ملزمتي قد قدمنا إليكم اليوم مقالنا عن قانون حجم ومساحة المكعب ونرجو أن يكون المقال نال إعجابكم.
