ما هي الأعداد الحقيقية؟
تعتبر الرياضيات واحدة من بين العلوم التي تعتبر معروفة بالنسبة للجميع بالمعنى المتعارف عليه الآن كمادة علمية كما هو موجود الآن، لكن هذا الأمر لا يعني أن الرياضيات من بين الأشياء التي كانت معروفة بين الأفراد.
مقدمة عن ما هي الأعداد الحقيقية؟
حيث أن الأشخاص كانوا يستخدمون الأرقام في العمليات التجارية التي يقوموا بها فيما بين بعضهم.
حيث أن التجارة تعتبر من بين أبرز الأعمال التي قد عرفها الشخص منذ أن بدأوا بالنشاط والعمل.
وكان نتيجة لذلك من المتوقع أن يتم استخدام تلك الأعداد، حيث تعتبر الأعداد بمثابة أسماء الأشخاص فلا يمكن أن يكون الشخص بلا اسم وهوية.
يستطيع أن يتعاونوا أو يتحدثوا ويتعاملون مع بعضهم البعض بدون أن يكون هناك اسم يتم تميزه به بين الأشخاص وبعضهم البعض.
تعتبر الأعداد هي الأرقام التي قد تعرف عليه الإنسان في أولى استخدام علم الرياضيات كعلم منفصل بذاته.
وبالرغم من أن الأرقام لم تكن في شكلها التي تم تجسيم الرياضيات بها وتوظيف الرياضيات من خلالها.
بل والتعرف على إعداد لم تكن موجودة في السابق ولم يتم التعرف عليها.
الأعداد الحقيقية
الأعداد الحقيقة هي واحدة بين الأعداد الموجودة والمتعارف عليها والتي يمكنك استخدامها في العمليات الحسابية، كالقول بأن 2+2= 4.
كذلك عمليات الطرح مثل 3-2=1، وعمليات الضرب أيضاً 3*3=9 وكذلك عمليات القسمة.
هذه الأعداد تم استخدامها حتى بدون التعرف على الرياضيات والإبداع فيها والتوصل إليها واكتشاف مجالاتها المختلفة.
فهذه الأعداد قد عمل بها التجار منذ قدم البشرية، خاصة أنهم كانوا يعملون بمجال التجارة.
شاهد أيضًا: ما هي الأعداد الزوجية والأعداد الفردية
الأعداد الغير حقيقة
- لا تختلف الأعداد الغير حقيقية عن الأعداد الحقيقية فهي نفسها التي نقوم بالتعامل بها بصورة يومية في حياتنا.
- ولكن تم صياغتها بشكل أخر مثل اللانهاية لعدد معين ويطلق عليها نها ويتم دراستها في مادة الرياضيات.
- ونجد هناك أيضاً اللوغاريتمات من بين الأعداد الغير حقيقة والتي يتم دراستها أيضاً في مادة الرياضيات فنجد هناك صيغة تقوم بطلب إحضار رقم والطلب.
- بإتيان اللوغاريتم لهذا الرقم مثل ويرمز لها بالرمز لو، والجذر التربيعي للعدد السالب 1.
- هذا العدد بالأساس ليس له جذر تربيعي، وبالتالي الجذر التربيعي للعدد السالب هو غير موجود.
معادلات رياضية معقدة
كثيراً ما نجد هناك العديد من المسائل الرياضية، التي قد تجدها صعبة عندما نسير في حلها قد نجد أن من خلال الخطوات لا نستطيع أن نخرج بعدد صحيح.
حتى قد نظن ان النتيجة خاطئة ولكن بعد جهود العلماء قد تم التوصل إلى أن المسائل الرياضية والمعادلات الرياضية، قد يكون أغلبها يقع في النتيجة عدد غير حقيقي.
عندما نقف أما مسألة رياضية معقدة وغير صحيحة هذه المسألة لا تعنى أنها لا يمكن حلها.
بل سيتم حلها، ولكن الناتج لهذه العملية الحسابية لن يكون عدد صحيح حقيقي مثل 1*1=1 هنا الناتج عدد حقيقي واضح صحيح.
أما في عملية أخرى وليكن قسمة العدد 9 على ستة النتيجة هنا لن تكن عدد صحيح حقيقي.
كما في العملية السابقة بل ستكن تقريبية غير صريحة ولا يمكن اعتبار الناتج عدد حقيقي.
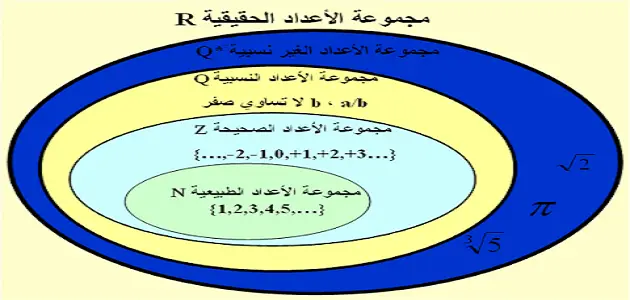
تقسيم الأعداد
الأعداد الطبيعية
تبدأ الأعداد الطبيعية من الرقم 1،2،3،4،5 إلى ما لا نهاية من الأعداد ولم يتم وضع نهاية للأعداد الطبيعية.
حتى وقتنا هذا فهي تزداد وتتضاعف على حسب تضاعف الأعداد وضربها وجمعها مع غيرها من الأعداد الأخرى.
الأعداد الصحيحة: تم التعرف على الأعداد الصحيحة بعد اعتبار الصفر عدد يبدأ منه بداية الأعداد، وأن وجود هذا العدد في بداية أي رقم كسابق عليه أو في منتصفه.
فإنه يغير من القيمة العددية للرقم بصورة مختلفة تماماً وأن الصفر يمكن إغفاله فقط عندما يوضع في نهاية الرقم أو على شمال العدد المذكور.
ومن بعد اكتشاف العدد فإنه تم التوصل إلى الأعداد السالبة وأبحت الأعداد الصحيحة تتكون من 0،1،2،3 من جهة اليمين، و تبدأ من 0،-1،-2 إلى نهاية الأعداد من جهة الشمال.
تابع أيضًا: طريقة تقسيم الأعداد العشرية
الأعداد النسبية
هي الأعداد التي يتم كتابتها على صورة كسر مثل 2\7 أو 8.88.
وهكذا فإن هذه الأعداد تعتبر نسبية غير صريحة مثل الأعداد التي تتكون من رقم مباشر مثل 33 أو 5 أو ما شابه ذلك.
ما هي الما لا نهاية
كل عدد من مجموعات الأعداد سواء كان ينتمي للأعداد الحقيقية أو الأعداد الغير حقيقية أو الأعداد النسبية أو الصحيحة له ما لا نهاية.
أي أننا لا يمكن أن نبدأ العد من رقم 1،2 ثم نقول أن المئة هي النهاية أو مضاعفاتها فلا نهاية لهذا النوع من الأعداد.
كذلك عندما يوضع أمامنا كسر مثل 7\6 لا يمكن أن نذكر أن مضاعفة هذا العدد هو الوصول إلى النهاية.
فهذا النوع ليس له نهاية يمكن كتابته بشكل صريح.
ما هي الأعداد المتسامية
هناك بعض الأعداد الغير معروفة بالشكل التي نجد عليها الأعداد الأخرى، والتي يتم استخدامها بشكل مستمر.
ومن بين تلك الأعداد هو العدد النيبيري هذا العدد ليس شائعاً مثل باقي الأعداد، التي يتم استخدامها في العمليات الرياضية والحسابية والجبر.
فهذا العدد وإن تم استخدامه في مجال الجبر إلا أنه يقل استخدامه بالصورة، التي تتواجد عليها الأعداد الأخرى في الرياضيات والجبر.
بل يعتبر هذا النوع من الأعداد مجرد حلقة في السلسلة الرياضية تضع في نهاية السلسلة.
خاصية الانغلاق
هناك بعض الخواص التي تتمتع بها الأعداد الحقيقة ومن بين تلك الخواص هي خاصية الانغلاق.
أي أنه إذا تم جمع العدد 4 مع العدد 4 فإن الناتج سيكون 8.
أي أن الناتج لم يكن كسراً أو عدد تقريبي، بل الناتج أصبح هو أيضاً من ضمن الأعداد الحقيقة المعروفة والواضحة في تسلسل الأعداد.
اقرأ أيضًا: ما هي الأعداد الأولية في الرياضيات
الخاصية التجميعية
- تتسم الأعداد الحقيقية بالخاصية التجميعية وهذا ما قد تفقده الأعداد الغير حقيقية.
- بمعنى أن الترتيب في عملية الجمع لا يؤثر في الناتج الحاصل من تلك العملية.
- فلا يزيد الناتج من العملية أو ينقص بل يصبح كما هو.
- على سبيل المثال إذا قمنا بجمع العدد 8+4=12 فإن هذا الناتج لن يتغير إذا قمنا بتبديل الترتيب 4+8=12.
- فإن ذكر الرقم الثاني أولاً لأن يغير في الأمر بل الناتج بالنهاية واحد لن يتغير، كذلك الأمر بالنسبة للضرب لا يؤثر الترتيب في الناتج أيضاً.
- أي أن حاصل ضرب 5*2=10 هو نفس حاصل ضرب 2*5= 10 بالنهاية حاصل الضرب عدد حقيقي صريح.
- من المستحيل أن يتم تجميع أعداد حقيقة مع بعضها مهما طالت العملية التجميعية.
- وتكونت من مجموعة أقواس أن يكون الناتج سلبي أو يؤثر ترتيب هذه الأعداد على الناتج، ونفس الأمر بالنسبة لعملية الضرب.
خاتمة عن ما هي الأعداد الحقيقية؟
خاصية الهوية هي أحد الخواص التي تتمتع بها الأعداد الحقيقة ولا توجد في الأعداد الغير حقيقية .
حيث تختلف على حسب العمليات الحسابية فإذا قمنا بجمع عدد ما وليكن 7+0=7 هنا العدد صفر لن يؤثر في العملية التجميعية.
وظهر الرقم في نفس الناتج دون زيادة أو نقصان ونفس الأمر بالنسبة لعملية الطرح 7-0= 7، لكن يختلف الأمر بالنسبة للعمليات الأخرى بالنسبة إلى عمليات الضرب وعمليات القسمة.
