قانون مساحة سطح المخروط
قانون مساحة سطح المخروط تختلف الأشكال الهندسية حسب أبعادها، فعلى سبيل المثال هناك أشكالًا ذات أبعادًا ثلاثية، وهناك أشكالًا ذات أبعاد ثنائية، وغيرها من الأشكال المتنوعة مثل المربع، والمثلث، ومتوازي الأضلاع، والدائرة، والمخروط وغيرها من الأشكال الهندسية.
المخروط
- المخروط (Cone)، هو عبارة عن مجسم ذو قاعدة واحدة مسطحة دائرية الشكل، وله جانب واحد فقط منحني الشكل، وهذا الجانب على شكل مثلث قائم الزاوية، إذ يلتف جانب المخروط حول أحد ضلعيه الأقصر من الوتر، ويوجد أعلى المخروط نقطة مدببة تسمى رأس المخروط.
أقرأ أيضًا: بحث عن الأشكال الهندسية وخواصها
أنواع المخروط
- هناك نوعان من المخروط على حسب طول الراسم، فإذا كان طول جميع الرواسم المخروط متساوية، فانه (مخروط دائري قائم)، أما إذا كان هناك اختلاف في طول الرواسم للمخروط فإنه يسمى (المخروط الدائري).
- المساحة
- المساحة لأي شكل هندسي هي الجزء المحصور بين نطاق معين على سطح ما، ويتم قياس المساحة بوحدة المتر المربع.
- حساب مساحة المخروط
- المخروط القائم يتكون من قطاع دائري، إذ أن مساحة هذا القطاع الدائري تمثل المساحة الجانبية للمخروط القائم، بينما قاعدة المخروط عبارة عن دائرة، وحتى يتم حساب المساحة الكلية للمخروط القائم، يجب أن يتم حساب المساحة الجانبية، وحساب مساحة القاعدة أيضًا، وبهذا فإن:
- المساحة الكلية للمخروط القائم =
- والمساحة الجانبية+ مساحة القاعدة).
- المساحة الكلية للمخروط القائم =
- (مساحة القطاع الدائري+ مساحة القاعدة).
- والمساحة الكلية للمخروط القائم =
- (π×نق× ل+ π ×نق²).
- حيث أن
- ل: طول راسم المخروط
- نق: نصف قطر قاعدة المخروط.
- π : حيث أن قيمة π تساوي 22/7 ويساوي تقريباً (3.14).
- هذا ويمكن استخدام القانون التالي في حساب المساحة الجانبية للمخروط القائم كما يلي:
- قانون مساحة القطاع الدائري=
- (زاوية القطاع الدائري المركزية÷360 درجة) × مساحة الدائرة
- حيث أن الزاوية المركزية للقطاع الدائري=180درجة.
قانون مساحة سطح المخروط
بعض الأمثلة التي توضح كيفية حساب مساحة سطح المخروط القائم كما يلي:
مثال (1)
- ورقة على شكل نصف دائرة، قطرها يساوي 6.28 سم، فإذا علمت أنه تم تحويلها إلى مخروط قائم احسب المساحة الجانبية لهذا المخروط؟
الحل
- المساحة الجانبية للمخروط القائم= مساحة القطاع الدائري.
- المساحة الجانبية للمخروط القائم=
- (درجة 180÷360)×π×نق².
- المساحة الجانبية للمخروط القائم= 1/2×π×نق². المساحة الجانبية للمخروط القائم= 2/πنق².
- بما أن نق=القطر÷2، بالتالي فإن نق=3.14، وتعويض نصف القطر في القانون.
- ينتج أن:
- المساحة الجانبية للمخروط القائم=
- 2/(π ×3.14×3.14).
- المساحة الجانبية للمخروط القائم=π9298سم²، (الجواب بدلالة π).
- والمساحة الجانبية للمخروط = 4.9298×3.14.
- المساحة الجانبية للمخروط = 15.4796سم².
مثال(2)
- أوجد مساحة مجسم الكلية يمثل مخروط قائم، إذا علمت أن نصف قطر قاعدته يساوي7م، أما ارتفاعه فيساوي 24 م؟
الحل
- المساحة الكلية للمخروط القائم= المساحة الجانبية + مساحة القاعدة.
- المساحة الكلية للمخروط القائم =
- (π×نق× ل+ π ×نق²).
- يتم تعويض نصف القطر، والارتفاع بالقانون، فينتج أن:
- المساحة الكلية للمخروط القائم=
- (π×7× ل+ π ×7²).
- المساحة الكلية للمخروط القائم=
- (π×7× ل+ π ×49).
- ولإيجاد ل، نطبق نظرية فيثاغورس
(ل)² = (نق)²+ (ع)² (ل)² = - (7)²+ (24)² (ل)² = 625
- يتم أخذ الجذر التربيعي للطرفين، ينتج أن:
- طول الراسم=25 سم.
- يتم تطبيق قيمة راسم المخروط بالقانون:
- المساحة الكلية للمخروط القائم=
- (π×49+ π ×25×7)
- المساحة الكلية للمخروط القائم=
- (π49+ π 175)
- المساحة الكلية للمخروط القائم=π 224 م²،
- (الجواب بدلالةπ).
- هكذا يتم تعويض قيمة π
- هكذا المساحة الكلية للمخروط القائم=703.36م².
شاهد أيضًا: كيف نحسب المساحة والمحيط
مثال(3)
- هكذا إناء على شكل مخروط دائري قائم، نصف قطر قاعدته تساوي 15 سم، وطول راسمه يساوي 30سم، فإذا علمت أنه يراد تغطيته بورق تغليف احسب مساحة ورق التغليف اللازم لتغطية الإناء.
الحل
- المساحة الكلية للمخروط القائم= المساحة الجانبية + مساحة القاعدة.
- لمساحة الكلية للمخروط القائم =
- (π×نق× ل+ π ×نق²).
- المساحة الكلية للمخروط القائم =
- (π(²15)+ π 30×15)
- المساحة الكلية للمخروط القائم =
- (π225+ π 450).
- المساحة الكلية للمخروط القائم =675 π، (الجواب بدلالة باي).
- المساحة الكلية للمخروط القائم = 2.120 سم²
مثال(4)
- هكذا إذا علم أن المساحة الخارجية في سطح مخروط تساوي 800 سم²، ونصف قطر قاعدته تساوي 8 سم، فما طول الراسم فيه؟
الحل
- المساحة الخارجية للمخروط=
- (طول راسم المخروط× نصف قطر قاعدة المخروط× ط)+ (مربع نصف قطر القاعدة× ط).
- المساحة الخارجية للمخروط =
- ( ل× نق× ط)+ (نق2 × ط).
- 800= (ل×8 × 3.14)+ (8× 8× 3.14).
- 800= (25.12 ×ل)+ 200.96.
- 12× ل= 800- 200.96.
- 12× ل= 599.04. ل
- طول الراسم= 599.04÷ 25.12= 23.84 سم.
خطوات صنع مخروط باستخدام الورق
يمكن عمل مخروط باستخدام الورق أو من الكرتون بطريقة سهلة وبسيطة، من خلال اتباع عدة خطوات وهي كما يلي:
- هكذا يتم رسم دائرة على ورقة أو كرتون
- هكذا يتم قص الشكل الدائري من الورقة.
- ويتم أخذ قطاعًا دائريًا من الدائرة التي تم قصها، ويمكن تسمية الضلع الأول للقطاع الدائري م أ ، والضلع الثاني م ب، أما القوس فهو أ ج ب.
- هكذا يتم لف القطاع بحيث يتطابق م ب مع م أ تمامًا، ثم يتم تثبيتها بدقة باستخدام اللاصق.
هكذا يتم تثبيت القوس أ ج ب، كقاعدة دائرية للمخروط، وينتج مخروط دائري، يحتوي على ما يلي:
- النقطة م هي رأس المخروط أ م تمثل راسم المخروط.
- القوس أ ج د هو عبارة عن قاعدة المخروط
- (ع ) تمثل ارتفاع المخروط، حيث أن (ع) يساوي طول (م د)، علمًا بأن النقطة (م) هي رأس المخروط أما النقطة (د) فهي عبارة عن مركز قاعدة المخروط (مركز الدائرة).
- هكذا بما أن م أ طول الراسم، و م د الارتفاع فإن أد نصف القطر، وعند إيصال خط مستقيم بين هذه النقاط فإنه ينتج مثلث قائم الزاوية عند النقطة د.
- ومن خلال هذه المعلومة يمكن التوصل لطول الضلع المجهول(غير المعروف) سواء كان هذا الضلع المجهول هو الارتفاع أو طول الراسم من خلال تطبيق نظرية فيثاغورس للمثلث القائم الزاوية.
- (أب) ² + (ب ج) ² = (أ ج) ² ، حيث أن أب و ب ج هما ضلعي المثلث القائم، وأج هو الوتر.
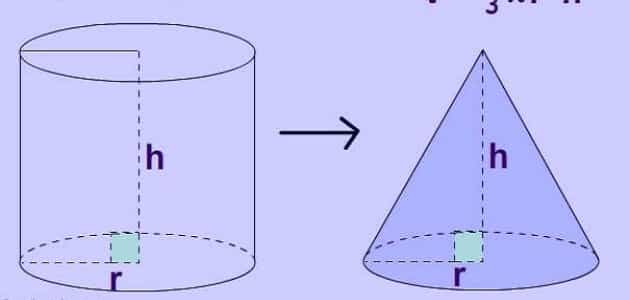
حجم المخروط - هكذا يلاحظ أن إذا تم إحضار أسطوانة ومخروط لهما نفس القاعدة والارتفاع، وكان المطلوب هو تعبئة هذه الأسطوانة بالرمل عن طريق استخدام المخروط.
- هكذا فإنه يتم ملاحظة أن الأسطوانة ستمتلئ بالرمل بعد تعبئة المخروط بالرمل ثلاثة مرات وسكبه بالأسطوانة، ومن هنا يستنتج أن حجم الأسطوانة يساوي ثلاثة مرات حجم المخروط الذي يشترك معها في نفس الارتفاع والقاعدة.
- وبناءاً عليه فإن:
- قانون حجم المخروط=
- ⅓ حجم الأسطوانة المتساوية معه بنفس الارتفاع والقاعدة.
إذًا
- حجم المخروط= ⅓ π ×نق²×ع.
- هكذا أمثلة حساب حجم المخروط
- هكذا بعض الأمثلة التي توضح كيفية حساب حجم المخروط وهي كما يلي:
مثال(1)
- هكذا احسب حجم مجسم على شكل مخروط، إذا علمت أن طول قاعدته يساوي 24 سم، أما ارتفاعه يساوي 16 سم؟
الحل
- حجم المخروط= ⅓ π ×نق²×ع.
- هكذا يتم تعويض قيمة نق=12 والارتفاع=16 بالقانون، ينتج أن: حجم المخروط= ⅓ π ×نق²×ع حجم المخروط= ⅓ × (π 16×(12²
- حجم المخروط= ⅓ × π 16×12×12
- هكذا إذًا: حجم المخروط= 768 πسم³،
- (الجواب بدلالة π)، يتم تعويض π يكون الناتج
- (52 .2411).
المخروط الناقص
- المخروط النّاقص هو أحد أشكال المخروط ولكن بدون رأس، فهو مخروط كامل تم قطع به مواز للقاعدة فهذا القطع يزيل رأس المخروط ولذلك أطلق عليه ناقصًا.
- هكذا وتختلف القطوع المخروطية التي تنتج من قطع المخروط إلى ثلاثة قطوع حسب موضع القطع من المخروط، وهي القطع المكافئ، والقطع الزائد، والقطع الناقص.
موضوعات اخرى مميزة:
هكذا نختم معكم اليوم مقالنا عن قانون مساحة سطح المخروط ونرجو أن يكون المقال قد نال إعجابكم، لا تنسوا لايك وشير للمقال لتعم الفائدة على الجميع.
